Dissipative function
dissipation function
A function used to take into account the effect of the forces of viscous friction on the motion of a mechanical system. The dissipation function describes the rate of decrease of the mechanical energy of the system; it is also used, more generally, to allow for the transition of energy of ordered motion to energy of disordered motion (ultimately to thermal energy).
The dissipation function for an isotropic medium, referred to unit volume, has the form
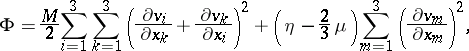 |
where  are the components of the tensor of the deformation rates and
are the components of the tensor of the deformation rates and  and
and  are the viscosity coefficients which describe the viscosity during motion and the viscosity during volume expansion, respectively.
are the viscosity coefficients which describe the viscosity during motion and the viscosity during volume expansion, respectively.
The equation of change of entropy in a viscous medium has the form:
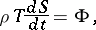 |
where  is the specific entropy,
is the specific entropy,  is the density and
is the density and  is the temperature of the liquid.
is the temperature of the liquid.
The dissipation function is a characterization of the viscous forces during the motion of a continuous medium. The equation of motion of a viscous medium is
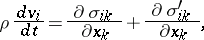 |
where the 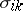 are the components of the friction-less part of the stress tensor, the
are the components of the friction-less part of the stress tensor, the
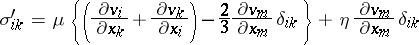 |
are the components of the "viscous" part of the stress tensor, and
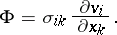 |
The dissipation function is employed to allow for the effect of the resistance to small vibrations of the system around its equilibrium position; to study the damping of vibrations in an elastic medium; to allow for heat losses during the damping of electric current vibrations in circuit systems; etc.
References
| [1] | L.D. Landau, E.M. Lifshitz, "Fluid mechanics" , Pergamon (1959) (Translated from Russian) |
Comments
For a Newtonian fluid the stress tensor has components 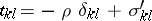 , where
, where 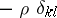 is the friction-less part (above called
is the friction-less part (above called 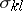 ) and
) and 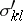 is the viscous part.
is the viscous part.
References
| [a1] | S.J. Pai, "Viscous flow theory" , 1. Laminar flow , v. Nostrand (1956) |
Dissipative function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dissipative_function&oldid=15366