Dirichlet principle
A method for solving boundary value problems for elliptic partial differential equations by reducing them to variational problems concerned with finding the minimum of certain functionals in certain classes of functions. In the narrow sense of the term, the Dirichlet principle reduces the first boundary value problem
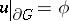 | (1) |
in a domain  with boundary
with boundary  for the Laplace equation
for the Laplace equation
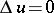 | (2) |
to finding the minimum of the Dirichlet integral
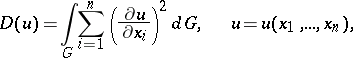 |
in the class of functions satisfying the condition
 | (3) |
and condition (1) (cf. Dirichlet variational problem).
The Dirichlet principle appeared and gained wide attention in the first half of the 19th century. It was used both for purely theoretical purposes — to demonstrate the existence and the uniqueness of solutions of boundary value problems — and in solutions of problems of practical importance. The most exact and complete formulation of the principle for the class of functions which are continuous together with their partial derivatives appears to have been given by P.G.L. Dirichlet himself in a course published in 1876 by one of his students. Dirichlet's proofs were incomplete; in particular, he failed to pose the problem of a giving proof of the existence of a minimum for the functional under consideration in the class of permissible functions, i.e. the functions meeting conditions (1) and (3). The work of Dirichlet was critized in the late 1860s by K. Weierstrass, who demonstrated, by means of an example, that the differential boundary value problem (1), (2) in the case of a continuous boundary function  may have a solution, while the corresponding variational problem need not have a solution owing to the fact that the Dirichlet integral for the solution of the problem (1), (2) becomes infinite in such a case. It was D. Hilbert who succeeded, at the end of the 19th century, to justify the Dirichlet principle on the assumption that there exists at least one permissible function. Subsequent advances in Dirichlet's principle are due to S.L. Sobolev, who showed that any function defined in an
may have a solution, while the corresponding variational problem need not have a solution owing to the fact that the Dirichlet integral for the solution of the problem (1), (2) becomes infinite in such a case. It was D. Hilbert who succeeded, at the end of the 19th century, to justify the Dirichlet principle on the assumption that there exists at least one permissible function. Subsequent advances in Dirichlet's principle are due to S.L. Sobolev, who showed that any function defined in an  -dimensional domain and having generalized partial derivatives of sufficiently high order and belonging to a space
-dimensional domain and having generalized partial derivatives of sufficiently high order and belonging to a space  ,
, 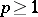 , in that domain, assumes real continuous boundary values on any sufficiently smooth
, in that domain, assumes real continuous boundary values on any sufficiently smooth  -dimensional manifold,
-dimensional manifold, 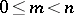 . In this way Sobolev could formulate and justify the Dirichlet principle for the poly-harmonic equation, including the case in which the boundary of the domain consists of manifolds of different dimensions.
. In this way Sobolev could formulate and justify the Dirichlet principle for the poly-harmonic equation, including the case in which the boundary of the domain consists of manifolds of different dimensions.
The appearance of Dirichlet's principle constituted an important stage in the development of the theory of boundary value problems for partial differential equations, representing as it did a novel approach to the theory. The Dirichlet principle, and all its possible modifications, are based, in the final count, on the reduction of the problem under study to some kind of variational problem, and have found extensive applications both in various fields of mathematics itself and in its applications. This is because the method can be used to demonstrate general theorems on solutions of equations, and also to obtain their concrete solutions in the form of limits of so-called minimizing sequences (i.e. sequences of permissible functions on which the values of the functional to be minimized tend to its minimum); also, numerical methods based on the construction of minimizing sequences are suitable for finding approximate solutions using an electronic computer.
Comments
The best-known method based on minimizing sequences is the Ritz method, see also [a1].
A historical account of Dirichlet's principle is given in [a2].
References
| [a1] | S.G. [S.G. Mikhlin] Michlin, "Numerische Realisierung von Variationsmethoden" , Akademie Verlag (1969) (Translated from Russian) |
| [a2] | A.F. Monna, "Dirichlet's principle: A mathematical comedy of errors and its influence on the development of analysis" , Oosthoek, Scheltema & Holkema (1975) |
| [a3] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [a4] | R. Courant, "Dirichlet's principle, conformal mapping, and minimal surfaces" , Interscience (1950) (With appendix by M. Schiffer: Some recent developments in the theory of conformal mapping) |
| [a5] | O.A. Ladyzhenskaya, N.N. Ural'tseva, "Equations aux dérivées partielles de type elliptique" , Dunod (1969) (Translated from Russian) |
| [a6] | V.P. Mikhailov, "Partial differential equations" , MIR (1978) (Translated from Russian) |
Dirichlet principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_principle&oldid=18701