Difference between revisions of "Dirichlet polynomial"
(Importing text file) |
(link to Dirichlet L-function) |
||
| Line 5: | Line 5: | ||
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202003.png" /> is a finite set of natural numbers, is called the Dirichlet polynomial with coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202004.png" /> (complex numbers) and exponents <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202005.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202006.png" /> is an increasing sequence of positive real numbers). In particular, Dirichlet polynomials are partial sums of corresponding [[Dirichlet series|Dirichlet series]]. | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202003.png" /> is a finite set of natural numbers, is called the Dirichlet polynomial with coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202004.png" /> (complex numbers) and exponents <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202005.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202006.png" /> is an increasing sequence of positive real numbers). In particular, Dirichlet polynomials are partial sums of corresponding [[Dirichlet series|Dirichlet series]]. | ||
| − | Dirichlet polynomials are extensively used and studied in analytic and multiplicative number theory (cf. also [[Analytic number theory|Analytic number theory]]). Most zeta-functions (cf. also [[Zeta-function|Zeta-function]]) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202007.png" />-functions (cf. also [[Dirichlet | + | Dirichlet polynomials are extensively used and studied in analytic and multiplicative number theory (cf. also [[Analytic number theory|Analytic number theory]]). Most zeta-functions (cf. also [[Zeta-function|Zeta-function]]) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202007.png" />-functions (cf. also [[Dirichlet L-function|Dirichlet <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202008.png" />-function]]), as well as their powers, can be approximated by Dirichlet polynomials, mostly with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d1202009.png" />. For example, uniformly for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d12020010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d12020011.png" />, the equality |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d12020012.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120200/d12020012.png" /></td> </tr></table> | ||
Revision as of 21:16, 9 January 2015
Let 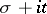 be a complex variable. A finite sum
be a complex variable. A finite sum
 |
where 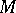 is a finite set of natural numbers, is called the Dirichlet polynomial with coefficients
is a finite set of natural numbers, is called the Dirichlet polynomial with coefficients 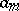 (complex numbers) and exponents
(complex numbers) and exponents 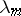 (
(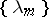 is an increasing sequence of positive real numbers). In particular, Dirichlet polynomials are partial sums of corresponding Dirichlet series.
is an increasing sequence of positive real numbers). In particular, Dirichlet polynomials are partial sums of corresponding Dirichlet series.
Dirichlet polynomials are extensively used and studied in analytic and multiplicative number theory (cf. also Analytic number theory). Most zeta-functions (cf. also Zeta-function) and 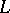 -functions (cf. also Dirichlet
-functions (cf. also Dirichlet 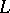 -function), as well as their powers, can be approximated by Dirichlet polynomials, mostly with
-function), as well as their powers, can be approximated by Dirichlet polynomials, mostly with 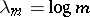 . For example, uniformly for
. For example, uniformly for 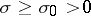 ,
, 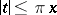 , the equality
, the equality
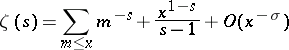 |
is valid for the Riemann zeta-function [a6]. Dirichlet polynomials also occur in approximate functional equations of zeta-functions [a2], [a6], and have a great influence on their analytic properties. A sufficient condition [a6] for the Riemann hypothesis (cf. Riemann hypotheses) is that the Dirichlet polynomial 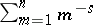 should have no zeros in
should have no zeros in 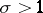 .
.
There exist inversion formulas for Dirichlet series (see, for example, [a2]), which give an integral expression of the Dirichlet polynomial 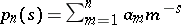 by a sum of corresponding Dirichlet series.
by a sum of corresponding Dirichlet series.
In applications, mean-value theorems for Dirichlet polynomials are very useful. The Montgomery–Vaughan theorem [a5] is the best of them, and has, for 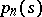 , the form
, the form
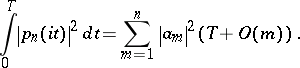 |
Transformation formulas for special Dirichlet polynomials were obtained by M. Jutila [a3].
Dirichlet polynomials have a limit distribution in the sense of weak convergence of probability measures. For example, let 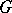 be a region on the complex plane, let
be a region on the complex plane, let 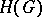 denote the space of analytic functions on
denote the space of analytic functions on 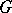 equipped with the topology of uniform convergence on compacta, let
equipped with the topology of uniform convergence on compacta, let 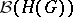 stand for the class of Borel sets of
stand for the class of Borel sets of 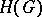 (cf. also Borel set), and let
(cf. also Borel set), and let 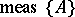 be the Lebesgue measure of the set
be the Lebesgue measure of the set  . Then [a4] there exists a probability measure
. Then [a4] there exists a probability measure 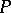 on
on 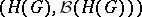 such that the measure
such that the measure
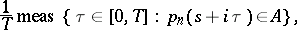 |
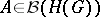 , converges weakly to
, converges weakly to 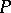 as
as 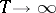 .
.
Dirichlet polynomials 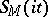 (with arbitrary real numbers
(with arbitrary real numbers 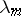 ) play an important role in the theory of almost-periodic functions (cf. also Almost-periodic function) [a1].
) play an important role in the theory of almost-periodic functions (cf. also Almost-periodic function) [a1].
References
| [a1] | A. Besicovitch, "Almost periodic functions" , Cambridge Univ. Press (1932) |
| [a2] | A. Ivič, "The Riemann zeta-function" , Wiley–Interscience (1985) |
| [a3] | M. Jutila, "Transformation formulae for Dirichlet polynomials" J. Number Th. , 18 : 2 (1984) pp. 135–156 |
| [a4] | A. Laurinčikas, "Limit theorems for the Riemann zeta-function" , Kluwer Acad. Publ. (1996) |
| [a5] | H.L. Montgomery, R.C. Vaughan, "Hilbert's inequality" J. London Math. Soc. , 8 : 2 (1974) pp. 73–82 |
| [a6] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1986) (Edition: Second) |
Dirichlet polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_polynomial&oldid=36171