Dirichlet Laplacian
Dirichlet–Laplace operator
In a broad sense, a restriction of the Laplace operator to the space of functions satisfying (in some sense) homogeneous Dirichlet boundary conditions. For an open set  in
in  , the Dirichlet Laplacian is usually defined via the Friedrichs extension procedure. Namely, first consider the (negative) Laplace operator
, the Dirichlet Laplacian is usually defined via the Friedrichs extension procedure. Namely, first consider the (negative) Laplace operator  defined on the subspace
defined on the subspace  of all infinitely smooth functions with compact support in
of all infinitely smooth functions with compact support in  . This is a symmetric operator, and the associated quadratic form (with the same domain
. This is a symmetric operator, and the associated quadratic form (with the same domain  ) is given by the Dirichlet integral
) is given by the Dirichlet integral
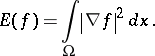 | (a1) |
Then the form  is closeable with respect to the norm
is closeable with respect to the norm
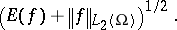 |
The domain of its closure 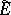 is the Sobolev space
is the Sobolev space  . Then
. Then 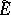 (given again by the right-hand side of (a1)) is the quadratic form of a non-negative self-adjoint operator (denoted by
(given again by the right-hand side of (a1)) is the quadratic form of a non-negative self-adjoint operator (denoted by 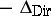 ); moreover,
); moreover,
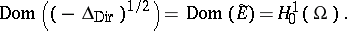 |
The operator 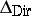 (sometimes taken with the minus sign) is called the Dirichlet Laplacian (in the weak sense).
(sometimes taken with the minus sign) is called the Dirichlet Laplacian (in the weak sense).
If  is bounded domain with boundary
is bounded domain with boundary  of class
of class 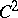 , then
, then
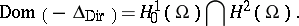 |
The Dirichlet Laplacian for a compact Riemannian manifold with boundary is defined similarly.
For a bounded open set  in
in  ,
,  is a positive unbounded linear operator in
is a positive unbounded linear operator in  with a discrete spectrum (cf. also Spectrum of an operator). Its eigenvalues
with a discrete spectrum (cf. also Spectrum of an operator). Its eigenvalues  (written in increasing order with account of multiplicity) can be found using the Rayleigh–Ritz variational formula (or max-min formula)
(written in increasing order with account of multiplicity) can be found using the Rayleigh–Ritz variational formula (or max-min formula)
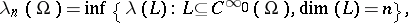 |
where
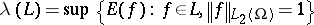 |
for a finite-dimensional linear subspace 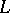 of
of  . It follows from the Rayleigh–Ritz formula that the eigenvalues
. It follows from the Rayleigh–Ritz formula that the eigenvalues 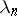 are monotonically decreasing functions of
are monotonically decreasing functions of  . See also [a3] for a survey of the asymptotic behaviour of the eigenvalues of the Dirichlet Laplacian and operators corresponding to other boundary value problems for elliptic differential operators.
. See also [a3] for a survey of the asymptotic behaviour of the eigenvalues of the Dirichlet Laplacian and operators corresponding to other boundary value problems for elliptic differential operators.
References
| [a1] | E.B. Davies, "Spectral theory and differential operators" , Cambridge Univ. Press (1995) |
| [a2] | D.E. Edmunds, W.D. Ewans, "Spectral theory and differential operators" , Clarendon Press (1987) |
| [a3] | Yu. Safarov, D. Vassiliev, "The asymptotic distribution of eigenvalues of partial differential operators" , Transl. Math. Monogr. , 55 , Amer. Math. Soc. (1997) |
Dirichlet Laplacian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_Laplacian&oldid=11906