Dirichlet L-function
Dirichlet 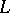 -series,
-series,  -series
-series
A function of a complex variable 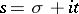 that is defined for any Dirichlet character
that is defined for any Dirichlet character 
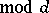 by the series
by the series
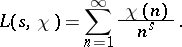 | (1) |
As functions of a real variable these were introduced by P.G.L. Dirichlet [1] in 1837 in the context of the proof that the number of primes in an arithmetic progression 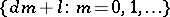 , where the difference
, where the difference  and the first term
and the first term 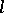 are relatively prime numbers, is infinite. They are a natural generalization of the Riemann zeta-function
are relatively prime numbers, is infinite. They are a natural generalization of the Riemann zeta-function 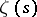 to an arithmetic progression and are a powerful tool in analytic number theory [2]–[4].
to an arithmetic progression and are a powerful tool in analytic number theory [2]–[4].
The series (1), known as a Dirichlet series, converges absolutely and uniformly in any bounded domain in the complex  -plane for which
-plane for which 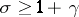 ,
, 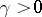 . If
. If 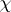 is a non-principal character, one has
is a non-principal character, one has
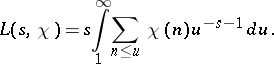 | (2) |
Since the sum in the integrand is bounded, this formula gives an analytic continuation of 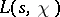 to a regular function in the half-plane
to a regular function in the half-plane 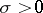 .
.
For any 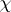
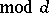 it is possible to represent
it is possible to represent 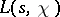 as an Euler product over prime numbers
as an Euler product over prime numbers 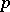 :
:
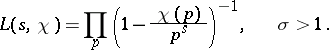 | (3) |
Hence, if 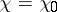 is a principal character
is a principal character 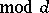 , one has, for
, one has, for 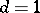 ,
,
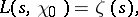 |
and for 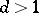 ,
,
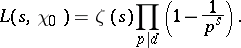 |
For this reason the properties of 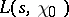 in the entire complex plane are mainly determined by the properties of
in the entire complex plane are mainly determined by the properties of 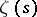 . In particular, the function
. In particular, the function 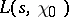 is regular for all
is regular for all  , except for
, except for 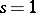 where it has a simple pole with residue
where it has a simple pole with residue 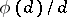 ; here
; here 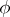 is Euler's function. If, on the other hand,
is Euler's function. If, on the other hand, 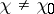 and if
and if 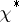 is the primitive character inducing the character
is the primitive character inducing the character 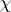
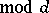 , then
, then
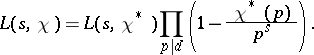 | (4) |
Thus, it is no essential restriction to consider only Dirichlet 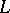 -functions for primitive characters. This property of Dirichlet
-functions for primitive characters. This property of Dirichlet 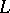 -functions is important, since many results concerning
-functions is important, since many results concerning 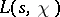 have a simple form for primitive characters only. If
have a simple form for primitive characters only. If 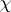
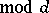 is primitive, the analytic continuation to the entire plane and the functional equation for the function
is primitive, the analytic continuation to the entire plane and the functional equation for the function 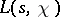 are obtained by direct generalization of Riemann's method for
are obtained by direct generalization of Riemann's method for 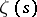 . Putting
. Putting
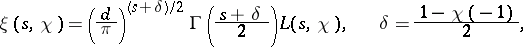 |
the result has the form
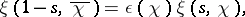 | (5) |
where  is the gamma-function,
is the gamma-function, 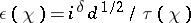 ,
, 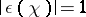 ,
,  is a Gauss sum, and
is a Gauss sum, and 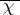 is the complex conjugate character to
is the complex conjugate character to 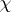 . This equation is known as the functional equation of the function
. This equation is known as the functional equation of the function 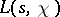 . It follows from this formula and from formulas (2) and (4) that the functions
. It follows from this formula and from formulas (2) and (4) that the functions 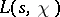 and
and 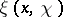 are entire functions for all
are entire functions for all 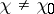 ; if
; if 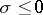 ,
, 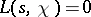 only at the points
only at the points 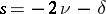 ,
, 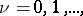 and at the points
and at the points  where the product in (4) vanishes; these points are known as the trivial zeros of
where the product in (4) vanishes; these points are known as the trivial zeros of 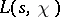 . The remaining zeros of
. The remaining zeros of 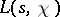 are said to be the non-trivial zeros. If
are said to be the non-trivial zeros. If 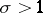 , then
, then 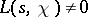 . Ch.J. de la Vallée-Poussin showed that
. Ch.J. de la Vallée-Poussin showed that 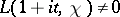 , so that all non-trivial zeros of a Dirichlet
, so that all non-trivial zeros of a Dirichlet 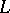 -function lie in the domain
-function lie in the domain 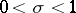 , which is known as the critical strip.
, which is known as the critical strip.
The distribution of the non-trivial zeros, and of the values of 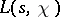 in the critical strip in general, is the most important problem in the theory of Dirichlet
in the critical strip in general, is the most important problem in the theory of Dirichlet 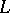 -functions, and is of fundamental importance in number theory.
-functions, and is of fundamental importance in number theory.
That each function 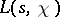 has infinitely many non-trivial zeros, and that the laws governing the distribution of primes in arithmetic progressions directly depend on the distribution of these zeros, is shown by the corresponding analogues of Riemann's formulas. In fact, let
has infinitely many non-trivial zeros, and that the laws governing the distribution of primes in arithmetic progressions directly depend on the distribution of these zeros, is shown by the corresponding analogues of Riemann's formulas. In fact, let 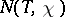 be the number of zeros of the function
be the number of zeros of the function 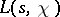 with a primitive character
with a primitive character 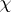
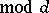 in the rectangle
in the rectangle 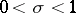 ,
, 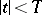 ,
, 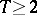 . Then
. Then
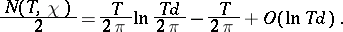 |
Let 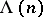 be the Mangoldt function,
be the Mangoldt function, 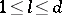 ,
, 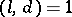 , and let
, and let
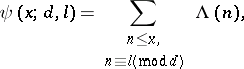 |
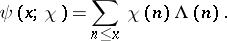 |
Then it follows from the orthogonality property of the characters that
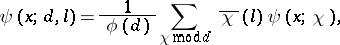 | (6) |
where the summation is extended over all characters 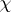
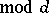 . Moreover, for a primitive character
. Moreover, for a primitive character  and for
and for 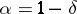 :
:
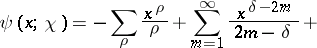 |
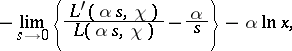 |
where  runs through the non-trivial zeros of
runs through the non-trivial zeros of 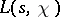 , and
, and 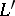 is the derivative of
is the derivative of 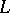 with respect to
with respect to  .
.
Approximate formulas for 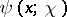 are more useful in practice: For arbitrary
are more useful in practice: For arbitrary 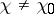 and for
and for 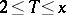 one has
one has
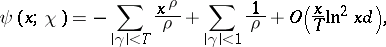 | (7) |
and for 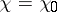 ,
,
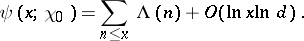 | (8) |
The quantity in (8) is the principal term of the sum in (6).
According to the so-called extended Riemann hypothesis, all non-trivial zeros of a Dirichlet  -function lie on the straight line
-function lie on the straight line 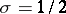 . If this hypothesis is valid, one has, for
. If this hypothesis is valid, one has, for 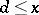 ,
,
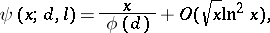 |
and many other important problems in number theory would have their final solution. However, problems concerning the distribution of the non-trivial zeros of a Dirichlet 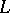 -function are exceptionally difficult, and relatively little is yet (1988) known on the subject. Stronger results were obtained for complex rather than for real characters.
-function are exceptionally difficult, and relatively little is yet (1988) known on the subject. Stronger results were obtained for complex rather than for real characters.
A generalization of the method proposed in 1899 by de la Vallée-Poussin for the function 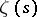 yields a bound on the non-trivial zeros of
yields a bound on the non-trivial zeros of 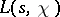 : For a complex character
: For a complex character 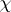
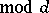 there exists an absolute constant
there exists an absolute constant 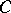 such that
such that 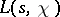 has no zeros in the domain
has no zeros in the domain
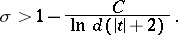 |
However, if 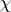 is a real non-principal character modulo
is a real non-principal character modulo 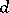 , then
, then 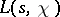 may have in this domain at most one simple real (
may have in this domain at most one simple real (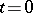 ) zero, known as the exceptional zero of
) zero, known as the exceptional zero of 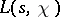 . The following inequality was deduced for the exceptional zero
. The following inequality was deduced for the exceptional zero 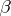 from the analytic class number formula for quadratic fields:
from the analytic class number formula for quadratic fields:
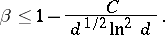 |
A well-known best (pre 1975) bound for 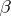 was obtained in 1935 by C.L. Siegel: For any
was obtained in 1935 by C.L. Siegel: For any 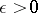 there exists a positive number
there exists a positive number 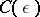 such that
such that
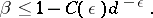 |
However, this estimate has the major drawback of being ineffective in the sense that the knowledge of  is insufficient to make an estimate for the numerical constant
is insufficient to make an estimate for the numerical constant 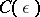 . This is also the disadvantage of the number-theoretic results based on Siegel's estimate.
. This is also the disadvantage of the number-theoretic results based on Siegel's estimate.
From the above bounds for the non-trivial zeros of Dirichlet 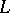 -functions and formulas (6)–(8), the following asymptotic law for the distribution of prime numbers can be derived:
-functions and formulas (6)–(8), the following asymptotic law for the distribution of prime numbers can be derived:
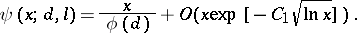 |
Here 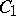 is an effectively computable constant for
is an effectively computable constant for 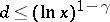 for some
for some 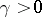 . Otherwise, one has
. Otherwise, one has 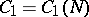 ineffectively, where
ineffectively, where 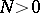 is such that
is such that 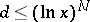 .
.
These results are the best results available in the problem of uniform distribution of prime numbers in arithmetic progressions with increasing difference 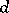 . A little more is known in the case where the value of
. A little more is known in the case where the value of 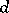 is fixed. In such a case the theory of Dirichlet
is fixed. In such a case the theory of Dirichlet 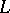 -functions for
-functions for 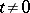 resembles in many respects the theory of the Riemann zeta-function [5], and the most recent bound on the zeros of
resembles in many respects the theory of the Riemann zeta-function [5], and the most recent bound on the zeros of 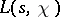 , obtained by the Vinogradov method for estimating trigonometric sums, has the form:
, obtained by the Vinogradov method for estimating trigonometric sums, has the form:
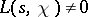 |
for
 |
where 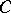 is a positive constant depending on
is a positive constant depending on 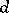 .
.
To this bound for the non-trivial zeros of Dirichlet 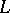 -functions modulo a fixed
-functions modulo a fixed 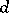 corresponds the best (1977) remainder term in the asymptotic formula for
corresponds the best (1977) remainder term in the asymptotic formula for 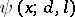 :
:
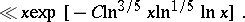 |
All formulas concerning the asymptotics of the function 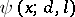 have analogues for the function
have analogues for the function 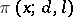 , viz. for the number of primes
, viz. for the number of primes 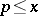 ,
, 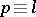 (
(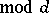 ), with principal term
), with principal term 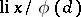 instead of
instead of 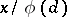 and a residual term which is smaller by a factor
and a residual term which is smaller by a factor 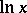 .
.
A major subject in modern studies on the theory of Dirichlet 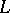 -functions is research on the density of the distribution of the non-trivial zeros of such functions. This research is concerned with giving estimates for the quantities
-functions is research on the density of the distribution of the non-trivial zeros of such functions. This research is concerned with giving estimates for the quantities
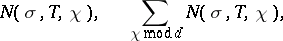 |
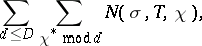 |
where 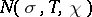 denotes the number of zeros of
denotes the number of zeros of 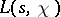 in the rectangle
in the rectangle 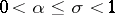 ,
, 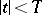 , and
, and 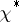 is a primitive character
is a primitive character 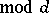 .
.
References
| [1] | P.G.L. Dirichlet, "Vorlesungen über Zahlentheorie" , Vieweg (1894) |
| [2] | H. Davenport, "Multiplicative number theory" , Springer (1980) |
| [3] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
| [4] | N.G. Chudakov, "Introductions to the theory of Dirichlet  -functions" , Moscow-Leningrad (1947) (In Russian) -functions" , Moscow-Leningrad (1947) (In Russian) |
| [5] | A. Walfisz, "Weylsche Exponentialsummen in der neueren Zahlentheorie" , Deutsch. Verlag Wissenschaft. (1963) |
| [6] | H. Montgomery, "Topics in multiplicative number theory" , Springer (1971) |
| [7] | A.F. Lavrik, "Development of the method of density of zeros of Dirichlet  -functions" Math. Notes , 17 : 5 (1975) pp. 483–488 Mat. Zametki , 17 : 5 (1975) pp. 809–817 -functions" Math. Notes , 17 : 5 (1975) pp. 483–488 Mat. Zametki , 17 : 5 (1975) pp. 809–817 |
Comments
The effective bound
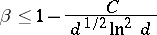 |
for the exceptional zero 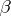 of
of 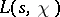 , where
, where 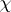 is a real non-principal character
is a real non-principal character 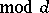 , was improved by D. Goldfeld and A. Schinzel [a1] to
, was improved by D. Goldfeld and A. Schinzel [a1] to
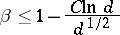 |
for 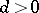 and
and
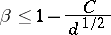 |
for 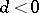 . Here
. Here 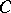 is an effectively computable constant. Using work of B.H. Gross and D. Zagier [a2] the result for
is an effectively computable constant. Using work of B.H. Gross and D. Zagier [a2] the result for 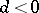 can be improved to
can be improved to
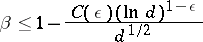 |
for any 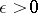 , where
, where 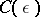 is an effective constant.
is an effective constant.
References
| [a1] | D. Goldfeld, A. Schinzel, "On Siegel's zero" Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) , 2 (1975) pp. 571–583 |
| [a2] | B.H. Gross, D. Zagier, "Heegner points and derivatives of  -series" Invent. Math. , 84 (1986) pp. 225–320 -series" Invent. Math. , 84 (1986) pp. 225–320 |
Dirichlet L-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_L-function&oldid=14351