Dimension of a partially ordered set
dimension of a poset
Let 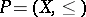 be a partially ordered set. A linear extension
be a partially ordered set. A linear extension 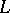 of
of 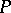 is a total ordering
is a total ordering 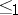 (see also Totally ordered set) on
(see also Totally ordered set) on 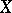 such that
such that 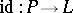 is order preserving, i.e. such that
is order preserving, i.e. such that 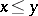 in
in 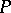 implies
implies 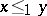 in
in 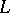 . The existence of linear extensions was proved by E. Szpilrain, [a4], in 1931.
. The existence of linear extensions was proved by E. Szpilrain, [a4], in 1931.
The dimension of a poset 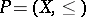 is the least
is the least 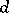 for which there exists a family of linear extensions
for which there exists a family of linear extensions 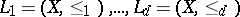 such that
such that
 |
A chain in 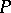 is a partially ordered subset of
is a partially ordered subset of 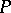 (a sub-poset) that is totally ordered. An anti-chain in
(a sub-poset) that is totally ordered. An anti-chain in  is a set of elements
is a set of elements  such that no
such that no 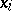 ,
, 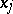 ,
, 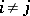 , are comparable. The height of
, are comparable. The height of 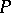 is the maximal length of a chain. The width of
is the maximal length of a chain. The width of 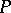 is the maximal size of an anti-chain. The Dilworth decomposition theorem says that if
is the maximal size of an anti-chain. The Dilworth decomposition theorem says that if 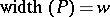 , then
, then 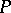 decomposes as the disjoint sum of
decomposes as the disjoint sum of 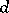 chains (cf. Disjoint sum of partially ordered sets; cf. also (the editorial comments to) Partially ordered set). Using this, T. Hiraguchi [a2] proved
chains (cf. Disjoint sum of partially ordered sets; cf. also (the editorial comments to) Partially ordered set). Using this, T. Hiraguchi [a2] proved
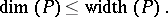 |
The concept 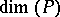 was introduced by B. Dushnik and E.W. Miler [a1].
was introduced by B. Dushnik and E.W. Miler [a1].
References
| [a1] | B. Dushnik, E.W. Miller, "Partially ordered sets" Amer. J. Math. , 63 (1941) pp. 600–610 |
| [a2] | T. Hiraguchi, "On the dimension of partially ordered sets" Sci. Rep. Kanazawa Univ. , 1 (1951) pp. 77–94 |
| [a3] | D. Kelley, W.T. Trotter, "Dimension theory for ordered sets" I. Rival (ed.) , Ordered Sets , Reidel (1987) pp. 171–212 |
| [a4] | E. [E. Szpilrain] Szpilrajn, "Sur l'extension de l'ordre partiel" Fund. Math. , 16 (1930) pp. 386–389 |
| [a5] | W.T. Trotter, "Partially ordered sets" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovász (ed.) , Handbook of Combinatorics , I , North-Holland (1995) pp. 433–480 |
Dimension of a partially ordered set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dimension_of_a_partially_ordered_set&oldid=17414