Differential equations with small parameter
A system of the type
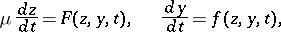 | (1) |
where  and
and 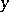 are, respectively,
are, respectively, 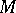 - and
- and  -dimensional vectors, and
-dimensional vectors, and  is a small parameter. If one puts, formally,
is a small parameter. If one puts, formally, 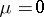 in (1), one obtains the so-called system of reduced equations
in (1), one obtains the so-called system of reduced equations
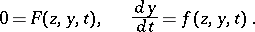 | (2) |
Let the solution 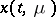 of (1) (
of (1) ( stands for the vector
stands for the vector 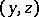 ) be defined by certain additional conditions. The clarification of the possibility of using equations (2) to construct an approximation to
) be defined by certain additional conditions. The clarification of the possibility of using equations (2) to construct an approximation to  which is asymptotic for small
which is asymptotic for small 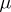 proves to be difficult owing to the fact that the system (2) is of a lower order than (1), so that its solution cannot meet all the conditions to be satisfied by (1). It is unclear a priori which of the additional conditions to be satisfied by (1) should be retained in defining the solution of (2) and which are to be discarded. Moreover, the equation
proves to be difficult owing to the fact that the system (2) is of a lower order than (1), so that its solution cannot meet all the conditions to be satisfied by (1). It is unclear a priori which of the additional conditions to be satisfied by (1) should be retained in defining the solution of (2) and which are to be discarded. Moreover, the equation 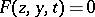 usually has several roots in
usually has several roots in  and, again, it is a priori unclear which of them is to be used in solving system (2) in order to obtain the correct approximation. These features constitute the difference between the problem of the asymptotics of the solution of (1) and the regular case in which
and, again, it is a priori unclear which of them is to be used in solving system (2) in order to obtain the correct approximation. These features constitute the difference between the problem of the asymptotics of the solution of (1) and the regular case in which 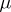 appears not as a coefficient of the derivatives, but appears regularly on the right-hand side.
appears not as a coefficient of the derivatives, but appears regularly on the right-hand side.
The first studies of systems such as (1) were concerned with the initial value problem
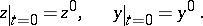 | (3) |
The most complete result was given by A.N. Tikhonov [1]; its main features are as follows. Let the equation 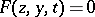 define a number of isolated roots
define a number of isolated roots
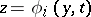 |
in some closed bounded domain 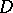 . Introduce the so-called associated system
. Introduce the so-called associated system
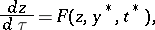 | (4) |
in which 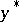 and
and 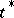 are considered as parameters. Take one of the roots
are considered as parameters. Take one of the roots 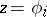 and denote it by
and denote it by  . The root
. The root 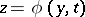 is said to be stable in
is said to be stable in 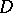 if for each point
if for each point 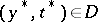 the corresponding rest point
the corresponding rest point 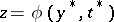 of the associated system (4) is asymptotically stable. The domain of influence of the stable root
of the associated system (4) is asymptotically stable. The domain of influence of the stable root 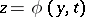 is the set of points
is the set of points 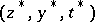 such that the solution of (4) defined by the initial condition
such that the solution of (4) defined by the initial condition 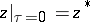 tends to
tends to 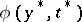 as
as 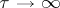 . It turns out that if
. It turns out that if 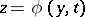 is a stable root, while the point
is a stable root, while the point 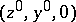 , which is the initial point for the solution
, which is the initial point for the solution  of the initial value problem (3), belongs to its domain of influence, then, as
of the initial value problem (3), belongs to its domain of influence, then, as 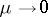 , the solution tends towards the solution of the system of reduced equations (2), the solution of the first equation in (2) is
, the solution tends towards the solution of the system of reduced equations (2), the solution of the first equation in (2) is 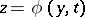 , while condition (3) is the initial condition for
, while condition (3) is the initial condition for 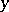 , but is discarded for
, but is discarded for  . In other words,
. In other words,
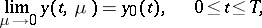 | (5) |
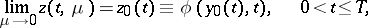 | (6) |
where 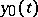 is found from the system
is found from the system
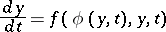 | (7) |
under the initial condition 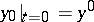 ;
; 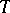 is connected with the dimension of
is connected with the dimension of 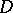 . Thus, unlike in the regular case, it is only under special conditions that the solution
. Thus, unlike in the regular case, it is only under special conditions that the solution 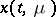 of (1) for small
of (1) for small  approaches the solution of the system in which
approaches the solution of the system in which 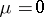 , i.e. system (2).
, i.e. system (2).
The limit transition (6) is not uniform since, in general, 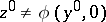 . In other words, owing to the "loss" of the initial conditions for
. In other words, owing to the "loss" of the initial conditions for  , a neighbourhood of
, a neighbourhood of 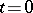 also contains a domain in which
also contains a domain in which 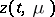 is not near to
is not near to 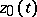 even though this domain unboundedly contracts as
even though this domain unboundedly contracts as 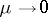 . The name of this effect is boundary layer, in analogy to an effect in hydrodynamics.
. The name of this effect is boundary layer, in analogy to an effect in hydrodynamics.
The concept of stability of a root 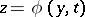 plays an important role in the study of (1). To the various stability criteria of the rest point according to Lyapunov (cf. Lyapunov stability) there correspond various stability criteria of the root
plays an important role in the study of (1). To the various stability criteria of the rest point according to Lyapunov (cf. Lyapunov stability) there correspond various stability criteria of the root 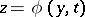 . The most useful one is the criterion of the first approximation, which requires that the eigen values
. The most useful one is the criterion of the first approximation, which requires that the eigen values 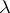 of the matrix
of the matrix
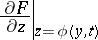 | (8) |
satisfy the inequality 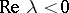 in
in 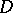 . If
. If 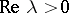 , then the result obtained for the problem (1), (3) is similar to that described above, but for
, then the result obtained for the problem (1), (3) is similar to that described above, but for 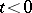 . If the matrix (8) has eigen values with real parts of opposite signs, i.e.
. If the matrix (8) has eigen values with real parts of opposite signs, i.e.
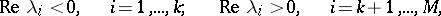 | (9) |
the solution of the initial problem (1), (3) usually has no limit as 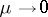 . However, if a boundary condition rather than an initial condition is stipulated for (1), if
. However, if a boundary condition rather than an initial condition is stipulated for (1), if 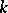 components of the vector
components of the vector  (components will be denoted by subscripts) are specified for
(components will be denoted by subscripts) are specified for  , while
, while 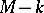 components of
components of  are specified for
are specified for 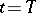 (the value of
(the value of 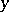 may be specified both for
may be specified both for 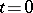 and
and 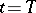 ),
),
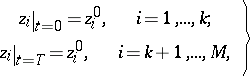 | (10) |
 | (11) |
then, if certain conditions are satisfied (in analogy to the requirement imposed on the initial value problem, i.e. that the initial point be contained in the domain of attraction of the stable root), then the limit transition (5), (6), where 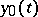 is defined as before by the system (7), applies to the solution
is defined as before by the system (7), applies to the solution 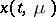 of the problem (1), (10), (11). The limit transition (6) applies for
of the problem (1), (10), (11). The limit transition (6) applies for 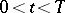 , and a boundary layer appears both in a neighbourhood of
, and a boundary layer appears both in a neighbourhood of 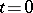 and in a neighbourhood of
and in a neighbourhood of 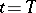 , since if
, since if 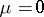 , the supplementary conditions (10), specified both for
, the supplementary conditions (10), specified both for 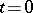 and
and 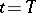 , are lost. Case (9) is known as the conditionally stable case [2].
, are lost. Case (9) is known as the conditionally stable case [2].
Following the establishment of the limit transitions (5), (6), studies were conducted with the purpose of obtaining an asymptotic expansion of its solution. In the regular case the solution of the initial value problem is represented as a power series in 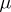 :
:
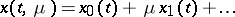 | (12) |
which is an asymptotic series if the right-hand sides are sufficiently smooth. In the case (1), owing to the presence of a boundary layer, the asymptotic expansion of the solution may be more complicated, since a so-called boundary-layer correction or boundary-layer series
 | (13) |
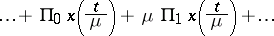 |
may have to be added to a power series of type (12). The terms 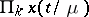 are known as the boundary-layer terms. They are significant near
are known as the boundary-layer terms. They are significant near 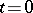 , after which they rapidly decrease in accordance with the law
, after which they rapidly decrease in accordance with the law 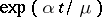 , where
, where 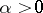 . A detailed description of an algorithm for the construction of an asymptotic expansion of the problem (1), (3) was given in [2], where it was proved that the remainder of the asymptotic expansion (13) is of the order
. A detailed description of an algorithm for the construction of an asymptotic expansion of the problem (1), (3) was given in [2], where it was proved that the remainder of the asymptotic expansion (13) is of the order 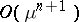 uniformly with respect to
uniformly with respect to 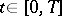 , provided that the right-hand sides of (1) are sufficiently smooth. A similar asymptotic expansion applies to the solution of the problem (1), (10), (11). The difference is that two boundary-layer corrections rather than one have to be added to the power series of the type (12), since a boundary layer is present both in a neighbourhood of
, provided that the right-hand sides of (1) are sufficiently smooth. A similar asymptotic expansion applies to the solution of the problem (1), (10), (11). The difference is that two boundary-layer corrections rather than one have to be added to the power series of the type (12), since a boundary layer is present both in a neighbourhood of 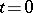 and in that of
and in that of 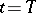 .
.
The asymptotic representation (13) (if a stable root exists) or the analogous representation with two boundary layers (if a conditionally stable root exists) makes it possible to prove the existence of and to obtain the asymptotics of the solution subject to supplementary conditions which are more complicated than (3) or (10), (11) [2]:
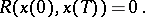 | (14) |
All the problems described above for constructing the function to which the unknown solution tends as 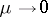 involved a single root
involved a single root 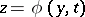 of the equation
of the equation 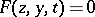 . However, if this equation has more than one root, one often observes the phenomenon of transition (or discontinuity). In this situation the solution of equation (1) which satisfies certain additional (in general, boundary) conditions is obtained in the limit as a curve (which is usually discontinuous), comprising several segments, each of which is defined, in the respective interval, by (2), when one of the roots
. However, if this equation has more than one root, one often observes the phenomenon of transition (or discontinuity). In this situation the solution of equation (1) which satisfies certain additional (in general, boundary) conditions is obtained in the limit as a curve (which is usually discontinuous), comprising several segments, each of which is defined, in the respective interval, by (2), when one of the roots 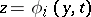 is suitably chosen as a solution of the equation
is suitably chosen as a solution of the equation 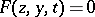 . As one passes from one interval to another, the root usually changes. The boundaries of the segments are known as the discontinuity points. In a neighbourhood of each such point a boundary layer is generated — so-called internal boundary layer. The causes of discontinuities may be very different. The asymptotics of the solution with discontinuity points may sometimes be described by an expansion of the type (13) [2] or may be more complicated (see, for instance, [3], [4]).
. As one passes from one interval to another, the root usually changes. The boundaries of the segments are known as the discontinuity points. In a neighbourhood of each such point a boundary layer is generated — so-called internal boundary layer. The causes of discontinuities may be very different. The asymptotics of the solution with discontinuity points may sometimes be described by an expansion of the type (13) [2] or may be more complicated (see, for instance, [3], [4]).
There exist numerous studies on individual, very different, problems such as the cases when  vanishes, the study of (1) on an infinite interval, the study of the solution of the initial value problem with initial
vanishes, the study of (1) on an infinite interval, the study of the solution of the initial value problem with initial  -values singular in
-values singular in 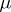 , the study of (1) in its abstract form, etc.; for a review, see [4]. A large number of studies are available on linear equations of the type (1). One of the typical problems in linear equations is the study of the asymptotics of the eigen values and the eigen functions , and the construction of asymptotics of the fundamental system of solutions in the large. The study of the last-named problem becomes very difficult if the system contains so-called turning points (cf. also Small parameter, method of the); for a detailed review of problems of this type see [4].
, the study of (1) in its abstract form, etc.; for a review, see [4]. A large number of studies are available on linear equations of the type (1). One of the typical problems in linear equations is the study of the asymptotics of the eigen values and the eigen functions , and the construction of asymptotics of the fundamental system of solutions in the large. The study of the last-named problem becomes very difficult if the system contains so-called turning points (cf. also Small parameter, method of the); for a detailed review of problems of this type see [4].
A number of results obtained for differential equations of the type (1) was applied to integro-differential equations with a small parameter (see, for example, [2]). There is also a large number of studies on partial differential equations containing a small parameter as coefficient of the leading derivative , [7], [10]. Perfectly similar asymptotic relationships are also noted for differential-difference equations with a small deviation of the argument [4].
Differential equations of the type (1), as well as other equations with a similar asymptotic behaviour of the solutions, are named singularly perturbed equations or singular perturbation problems, as distinct from the regular case. Singularly perturbed systems have been studied by the averaging method of Krylov–Bogolyubov, which can be particularly effective in the study of resonance phenomena and oscillation processes; the method of ascent or of regularization has also been proposed [8]. Singularly perturbed equations are also encountered in various domains of physics and technology: in the theory of non-linear oscillations, hydrodynamics, celestial mechanics, quantum mechanics, kinetics, etc. [11].
References
| [1] | A.N. Tikhonov, "Systems of differential equations containing a small parameter in front of the derivatives" Mat. Sb. , 31 : 3 (1952) pp. 575–586 (In Russian) |
| [2] | A.B. Vasil'eva, V.F. Butuzov, "Asymptotic expansions of solutions of singularly perturbed equations" , Moscow (1973) (In Russian) |
| [3] | E.F. Mishchenko, N.Kh. Rozov, "Differential equations with small parameters and relaxation oscillations" , Plenum (1980) (Translated from Russian) |
| [4] | V.F. Butuzov, A.B. Vasil'eva, M.V. Fedoryuk, "Asymptotic methods in the theory of ordinary differential equations" Itogi Nauk. Mat. Anal. 1967 (1969) pp. 5–75 (In Russian) |
| [5a] | M.I. Vishik, L.A. Lyusternik, "Regular degeneration and a boundary layer for linear differential equations with a small parameter" Uspekhi Mat. Nauk , 12 : 5 (1957) pp. 3–122 (In Russian) |
| [5b] | M.I. Vishik, L.A. Lyusternik, "The solution of some perturbation problems for matrices and selfadjoint or non-selfadjoint differential equations I" Russian Math. Surveys , 15 : 3 (1960) pp. 1–73 Uspekhi Mat. Nauk , 15 : 3 (1960) pp. 3–80 |
| [6] | M.I. Imanaliev, "Asymptotic methods in the theory of singularly perturbed integro-differential systems" , Frunze (1972) (In Russian) |
| [7] | V.A. Trenogin, "The development and applications of the asymptotic method of Lyusternik and Vishik" Russian Math. Surveys , 25 : 4 (1970) pp. 119–156 Uspekhi Mat. Nauk , 25 : 4 (1970) pp. 123–156 |
| [8] | S.A. Lomov, "Perturbation theory of singular boundary value problems" , Alma-Ata (1976) (In Russian) |
| [9] | S.A. Lomov, "Introduction to general singular perturbations theory" , Moscow (1981) (In Russian) |
| [10] | A.B Vasil'eva, "Singularly perturbed differential equations of parabolic type" F. Verhulst (ed.) , Asymptotic analysis II , Lect. notes in math. , 985 , Springer (1983) pp. 38–75 |
| [11] | , BAIL IV. Proc. Fourth Internat. Conf. on Boundary and Interior Layers Novosibirsk , Boole Press (1986) |
Comments
The technique discussed above to treat the solution by different expansions in the various layers is commonly referred to as the method of matched asymptotic expansions.
The list of references is rather outdated and totally ignores the Western literature. As a general monograph one can consult [a1], recent books on internal layers and relaxation oscillations are [a2], respectively [a3].
It should be noted that Tikhonov's original proof contains a small slip, discovered and amended by F. Hoppensteadt [a4] (see also [a1]). A recent treatise on the averaging method is [a5]. The method is, in general, not applicable to singular perturbation problems of type (1).
References
| [a1] | W. Eckhaus, "Asymptotic analysis of singular perturbations" , North-Holland (1979) |
| [a2] | K.W. Chang, F.A. Howes, "Nonlinear singular perturbation phenomena: theory and application" , Springer (1984) |
| [a3] | J. Grasman, "Asymptotic methods for relaxation oscillations and applications" , Springer (1987) |
| [a4] | F. Hoppensteadt, "Stability in systems with parameter" J. Math. Anal. Appl. , 18 (1967) pp. 129–134 |
| [a5] | J.A. Sanders, F. Verhulst, "Averaging methods in nonlinear dynamical systems" , Springer (1985) |
| [a6] | W. Eckhaus, "Matched asymptotic expansion and singular perturbations" , North-Holland & American Elsevier (1973) |
| [a7] | W. Eckhaus, E.M. de Jager, "Asymptotic solutions of singular perturbation problems for linear differential equations of elliptic type" Arch. Rational Mech. Anal. , 23 (1966) pp. 26–86 |
| [a8] | R.E. O'Malley, "Introduction to singular perturbations" , Acad. Press (1974) |
| [a9] | W. Wazov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965) |
Differential equations with small parameter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_equations_with_small_parameter&oldid=14948