Difference between revisions of "Diagram(2)"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 63 formulas out of 75 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 75 formulas, 63 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | Let $G$ and $G ^ { \prime }$ be directed graphs (also called oriented graphs, diagram schemes or pre-categories; cf. also [[Graph, oriented|Graph, oriented]]). A diagram of shape (also called a diagram of type) $G$ in $G ^ { \prime }$ is a morphism of graphs $d : G \rightarrow G ^ { \prime }$; i.e. if $G$ and $G ^ { \prime }$ are given by | ||
| − | + | \begin{equation*} G : A G \overset{\text{dom}_G}{\underset{\underset{\text{codom}_G}{\rightarrow} }{\rightarrow}} O G, \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120120/d1201209.png"/></td> </tr></table> |
| − | + | (here $O G$ and $A G$ denote, respectively, a set of objects and a set of arrows of $G$), then a morphism $d$ is a pair of mappings | |
| − | + | \begin{equation*} d _ { 0 } : O G \rightarrow O G ^ { \prime } , \quad d _ { A } : A G \rightarrow A G ^ { \prime } \end{equation*} | |
| − | + | with $\operatorname {dom}_{G^{\prime}} \circ d _ { A } = d _ { 0 } \circ \operatorname {dom}_{G}$, $\operatorname{codom}_{G'} \circ d _ { A } = d _ { 0 } \circ \operatorname{codom}_{G}$. | |
| − | + | A diagram is called finite if its shape is a finite [[Graph|graph]], i.e. $O G$ and $A G$ are finite sets. A diagram in a [[Category|category]] $\mathcal{C}$ is defined as a diagram $G \rightarrow U \mathcal{C}$, where $U \cal C$ denotes the underlying graph of $\mathcal{C}$ (with the same objects and arrows, forgetting which arrows are composites and which are identities). | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | Every [[Functor|functor]] $F : \mathcal{C} \rightarrow \mathcal{C} ^ { \prime }$ is also a diagram $U F : U \mathcal C \rightarrow U \mathcal C ^ { \prime }$ between the corresponding graphs. This observation defines the forgetful functor $U : \operatorname{Cat} \rightarrow \operatorname{Graph}$ from small categories to small graphs (cf. also [[Functor|Functor]]). |
| + | |||
| + | Let $d , d ^ { \prime } : G \rightarrow \mathcal{C}$ be two diagrams of the same shape $G$ in the same category $\mathcal{C}$. A morphism between $d$ and $d ^ { \prime }$ is a mapping $\Phi : O G \rightarrow A \mathcal{C}$ that carries each object $g$ of the graph $G$ to an arrow $\Phi g : d g \rightarrow d ^ { \prime } g$, such that for any arrow $a : g \rightarrow g ^ { \prime }$ of $G$ the diagram | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120120/d12012037.png"/></td> </tr></table> | ||
commutes. | commutes. | ||
| − | All diagrams of the shape | + | All diagrams of the shape $G$ in $\mathcal{C}$ and all morphisms between them form a category. |
| − | Let | + | Let $d : G \rightarrow \mathcal C$ be a diagram in the category $\mathcal{C}$ and let $\alpha = ( a _ { 1 } , \dots , a _ { n } )$ be a finite sequence of arrows of the graph $G$ with $\operatorname{dom} a_{i+1}=\operatorname{codom} a_i$, $i = 1 , \dots , n - 1$. Put $d \alpha = d a _ { n } \circ \ldots \circ d a _ { 1 }$. A diagram $d$ is called commutative if $d \alpha = d \alpha'$ for any finite sequence $\alpha ^ { \prime } = ( a ^ { \prime_1 } , \ldots , a ^ { \prime_m } )$ in $G$ with $\operatorname{dom} \alpha_{j+1}^{\prime} = \operatorname { codom } \alpha _ { j } ^ { \prime }$, $j = 1 , \dots , m - 1$, $\operatorname{dom} a_1= \operatorname { dom } a_1'$, $\operatorname{codom}a_n=\operatorname{codom}a_m'$. |
| − | A sequence is a diagram | + | A sequence is a diagram $d : G \rightarrow \mathcal C$, where $G$ is of the form |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120120/d12012057.png"/></td> </tr></table> |
The corresponding diagram is represented by | The corresponding diagram is represented by | ||
| − | + | \begin{equation*} c _ { 1 } \stackrel { \phi _ { 1 } } { \rightarrow } \ldots \stackrel { \phi _ { n - 1 } } { \rightarrow } c _ { n }, \end{equation*} | |
| − | where | + | where $c _ { k } = d ( g _ { k } )$ are objects and $\phi _ { k } = d ( a _ { k } )$ are arrows of $\mathcal{C}$. |
| − | A triangle diagram in the category | + | A triangle diagram in the category $\mathcal{C}$ is a diagram with shape graph |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120120/d12012063.png"/></td> </tr></table> |
and is represented as | and is represented as | ||
| − | + | \begin{equation*} \left. \begin{array} { c c c } { \square } & { c _ { 2 } } & { \square } \\ { \square } & { \square } & { \searrow ^ { \phi _ { 2 } } } \\ { \square ^ { \phi _ { 1 } } \nearrow } & { \vec { \phi _ { 3 } } } &{c_3} \end{array} \right. . \end{equation*} | |
| − | Commutativity means that | + | Commutativity means that $\phi _ { 2 } \circ \phi _ { 1 } = \phi _ { 3 }$. |
| − | A quadratic diagram (also called a square diagram) in | + | A quadratic diagram (also called a square diagram) in $\mathcal{C}$ corresponds to the graph |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120120/d12012067.png"/></td> </tr></table> |
and is represented as | and is represented as | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d120/d120120/d12012068.png"/></td> </tr></table> |
| − | Commutativity means | + | Commutativity means $\phi _ { 2 } \circ \phi _ { 1 } = \phi _ { 3 } \circ \phi _ { 4 }$. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Grothendieck, "Sur quelques points d'algebre homologique" ''Tôhoku Math. J. Ser. II'' , '''9''' (1957) pp. 120–221</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> S. Maclane, "Categories for the working mathematician" , Springer (1971)</td></tr></table> |
Revision as of 16:55, 1 July 2020
Let $G$ and $G ^ { \prime }$ be directed graphs (also called oriented graphs, diagram schemes or pre-categories; cf. also Graph, oriented). A diagram of shape (also called a diagram of type) $G$ in $G ^ { \prime }$ is a morphism of graphs $d : G \rightarrow G ^ { \prime }$; i.e. if $G$ and $G ^ { \prime }$ are given by
\begin{equation*} G : A G \overset{\text{dom}_G}{\underset{\underset{\text{codom}_G}{\rightarrow} }{\rightarrow}} O G, \end{equation*}
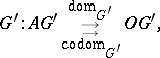 |
(here $O G$ and $A G$ denote, respectively, a set of objects and a set of arrows of $G$), then a morphism $d$ is a pair of mappings
\begin{equation*} d _ { 0 } : O G \rightarrow O G ^ { \prime } , \quad d _ { A } : A G \rightarrow A G ^ { \prime } \end{equation*}
with $\operatorname {dom}_{G^{\prime}} \circ d _ { A } = d _ { 0 } \circ \operatorname {dom}_{G}$, $\operatorname{codom}_{G'} \circ d _ { A } = d _ { 0 } \circ \operatorname{codom}_{G}$.
A diagram is called finite if its shape is a finite graph, i.e. $O G$ and $A G$ are finite sets. A diagram in a category $\mathcal{C}$ is defined as a diagram $G \rightarrow U \mathcal{C}$, where $U \cal C$ denotes the underlying graph of $\mathcal{C}$ (with the same objects and arrows, forgetting which arrows are composites and which are identities).
Every functor $F : \mathcal{C} \rightarrow \mathcal{C} ^ { \prime }$ is also a diagram $U F : U \mathcal C \rightarrow U \mathcal C ^ { \prime }$ between the corresponding graphs. This observation defines the forgetful functor $U : \operatorname{Cat} \rightarrow \operatorname{Graph}$ from small categories to small graphs (cf. also Functor).
Let $d , d ^ { \prime } : G \rightarrow \mathcal{C}$ be two diagrams of the same shape $G$ in the same category $\mathcal{C}$. A morphism between $d$ and $d ^ { \prime }$ is a mapping $\Phi : O G \rightarrow A \mathcal{C}$ that carries each object $g$ of the graph $G$ to an arrow $\Phi g : d g \rightarrow d ^ { \prime } g$, such that for any arrow $a : g \rightarrow g ^ { \prime }$ of $G$ the diagram
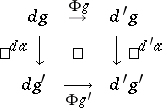 |
commutes.
All diagrams of the shape $G$ in $\mathcal{C}$ and all morphisms between them form a category.
Let $d : G \rightarrow \mathcal C$ be a diagram in the category $\mathcal{C}$ and let $\alpha = ( a _ { 1 } , \dots , a _ { n } )$ be a finite sequence of arrows of the graph $G$ with $\operatorname{dom} a_{i+1}=\operatorname{codom} a_i$, $i = 1 , \dots , n - 1$. Put $d \alpha = d a _ { n } \circ \ldots \circ d a _ { 1 }$. A diagram $d$ is called commutative if $d \alpha = d \alpha'$ for any finite sequence $\alpha ^ { \prime } = ( a ^ { \prime_1 } , \ldots , a ^ { \prime_m } )$ in $G$ with $\operatorname{dom} \alpha_{j+1}^{\prime} = \operatorname { codom } \alpha _ { j } ^ { \prime }$, $j = 1 , \dots , m - 1$, $\operatorname{dom} a_1= \operatorname { dom } a_1'$, $\operatorname{codom}a_n=\operatorname{codom}a_m'$.
A sequence is a diagram $d : G \rightarrow \mathcal C$, where $G$ is of the form
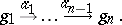 |
The corresponding diagram is represented by
\begin{equation*} c _ { 1 } \stackrel { \phi _ { 1 } } { \rightarrow } \ldots \stackrel { \phi _ { n - 1 } } { \rightarrow } c _ { n }, \end{equation*}
where $c _ { k } = d ( g _ { k } )$ are objects and $\phi _ { k } = d ( a _ { k } )$ are arrows of $\mathcal{C}$.
A triangle diagram in the category $\mathcal{C}$ is a diagram with shape graph
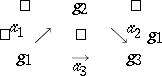 |
and is represented as
\begin{equation*} \left. \begin{array} { c c c } { \square } & { c _ { 2 } } & { \square } \\ { \square } & { \square } & { \searrow ^ { \phi _ { 2 } } } \\ { \square ^ { \phi _ { 1 } } \nearrow } & { \vec { \phi _ { 3 } } } &{c_3} \end{array} \right. . \end{equation*}
Commutativity means that $\phi _ { 2 } \circ \phi _ { 1 } = \phi _ { 3 }$.
A quadratic diagram (also called a square diagram) in $\mathcal{C}$ corresponds to the graph
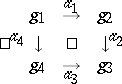 |
and is represented as
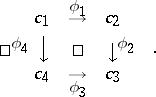 |
Commutativity means $\phi _ { 2 } \circ \phi _ { 1 } = \phi _ { 3 } \circ \phi _ { 4 }$.
References
| [a1] | P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967) |
| [a2] | A. Grothendieck, "Sur quelques points d'algebre homologique" Tôhoku Math. J. Ser. II , 9 (1957) pp. 120–221 |
| [a3] | S. Maclane, "Categories for the working mathematician" , Springer (1971) |
Diagram(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Diagram(2)&oldid=50101