Design with mutually orthogonal resolutions

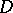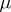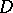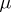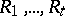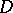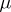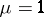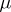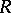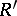A combinatorial design (cf. also Block design) with replication number is said to be -resolvable if the blocks of can be partitioned into classes (called -resolution classes) () such that each element of is contained in precisely blocks of each class. If , the design is called resolvable. Two -resolutions and of 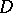are called orthogonal if 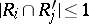for all 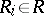, 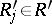. 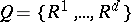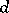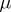(It should be noted that the blocks of the design are considered as being labeled so that if a subset of the element set occurs as a block more than once, the blocks are treated as being distinct.) A set of -resolutions of is called a set of mutually orthogonal -resolutions if the 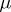-resolutions of 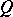are pairwise orthogonal. If 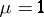, 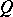is a set of mutually orthogonal resolutions. If 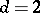and 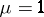, the design is called doubly resolvable.

The existence of a Room square of side is equivalent to the existence of a doubly resolvable 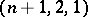-BIBD (cf. also Block design). The rows form one resolution and the columns form an orthogonal resolution. A Room -cube of side is a 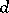-dimensional array, each cell of which either is empty or contains an unordered pair of elements, such that each two-dimensional projection is a Room square of side . The existence of a Room 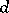-cube of side is equivalent to the existence of a set of 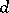mutually orthogonal resolutions of an 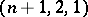-BIBD. A pair of orthogonal 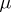-resolutions of a 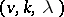-BIBD can also be used to construct an array, a Kirkman square .

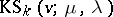An important open question in design theory is determining a good upper bound for 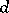, where 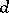is the size of the largest set of mutually orthogonal resolutions for a design. The case for Room cubes has received considerable attention. Let 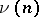denote the maximum 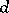for which there exists a Room -cube of side . A simple counting argument gives . However, evidence from small designs and constructions supports a conjecture (from 1973) that . This conjecture and a good upper bound for 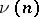remain open problems (1996), [a3].

In general, very little is known about the existence of designs with mutually orthogonal resolutions. Necessary and sufficient conditions are known for the existence of Kirkman squares with block size two and for Room squares; see [a3] for references. Results on Room 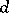-cubes can also be found in [a3]. Results for balanced incomplete block designs with block size 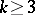can be found in [a2], [a4], [a6], and existence results and bounds for other types of designs can be found in [a7].

Partial resolutions can also be used in place of resolutions in the definitions above. Examples of such designs include 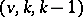-BIBDs with mutually orthogonal near resolutions (see [a5]) and frames which use group divisible designs (see [a3], [a4], [a5]).

For recent results on resolvable designs, see [a1].

The terminology has not yet been standardized for the arrays constructed from designs with mutually orthogonal resolutions. Generalized Room squares, Kirkman cubes, and multi-dimensional Kirkman arrays all refer to designs with mutually orthogonal resolutions.

References

[a1]	R.J.R. Abel, S.C. Furino, "Resolvable and near resolvable designs" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , CRC Handbook of Combinatorial Designs , CRC (1996) pp. 87–94
[a2]	C.J. Colbourn, A. Rosa, "Orthogonal resolutions of triple systems" Australasian J. Combin. , 12 (1995) pp. 259–269
[a3]	J.H. Dinitz, D.R. Stinson, "Room squares and related designs" J.H. Dinitz (ed.) D.R. Stinson (ed.) , Contemporary Design Theory: A Collection of Surveys , Wiley (1992) pp. 137–204
[a4]	E.R. Lamken, "The existence of doubly resolvable 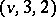-BIBDs" J. Combin. Th. A , 72 (1995) pp. 50–76
[a5]	E.R. Lamken, "The existence of doubly near resolvable 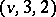-BIBDs" J. Combin. Designs , 2 (1994) pp. 427–440
[a6]	E.R. Lamken, "Constructions for resolvable and near resolvable -BIBDs" D.K. Ray-Chaudhuri (ed.) , Coding Theory and Design Theory. Part II. Design Theory , Springer (1990) pp. 236–250
[a7]	E.R. Lamken, S.A. Vanstone, "Designs with mutually orthogonal resolutions" European J. Combin. , 7 (1986) pp. 249–257