Dehn surgery
Let 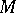 be a closed
be a closed  -dimensional manifold and let
-dimensional manifold and let 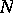 be a solid torus in the interior of
be a solid torus in the interior of 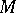 . Remove
. Remove  from
from 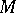 and glue in instead of it another solid torus
and glue in instead of it another solid torus 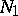 by a homeomorphism
by a homeomorphism  . One says that the resulting new
. One says that the resulting new  -dimensional manifold
-dimensional manifold
 |
is obtained from 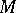 by a Dehn surgery. Note that
by a Dehn surgery. Note that 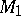 is determined by the following data: 1) a knot
is determined by the following data: 1) a knot 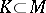 (a core circle
(a core circle 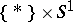 of the solid torus
of the solid torus 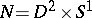 , cf. also Knot theory); and 2) a non-trivial simple closed curve
, cf. also Knot theory); and 2) a non-trivial simple closed curve 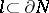 (the image under
(the image under 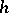 of a meridian of
of a meridian of 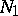 ). The Dehn surgery is called integer if
). The Dehn surgery is called integer if 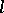 is a longitude of
is a longitude of 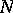 , i.e.,
, i.e., 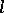 intersects a meridional curve of
intersects a meridional curve of  transversally in a single point.
transversally in a single point.
If 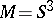 , then among all longitudes of
, then among all longitudes of 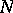 there is a preferred one, which bounds a surface in the complement of
there is a preferred one, which bounds a surface in the complement of 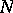 . The preferred longitude
. The preferred longitude 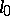 forms together with a meridian
forms together with a meridian 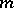 of
of 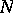 a coordinate system on
a coordinate system on 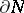 . Therefore,
. Therefore, 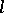 has the form
has the form 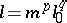 , where
, where 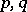 are coprime integers, and is determined by the rational number
are coprime integers, and is determined by the rational number 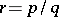 . The Dehn surgery is integer if and only if
. The Dehn surgery is integer if and only if  is an integer. This explains the terminology.
is an integer. This explains the terminology.
Let 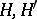 be two handle-bodies having the same genus (cf. Handle theory) and let
be two handle-bodies having the same genus (cf. Handle theory) and let  be a homeomorphism. Denote by
be a homeomorphism. Denote by 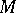 the closed
the closed  -dimensional manifold
-dimensional manifold 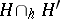 obtained by gluing
obtained by gluing 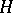 and
and 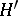 along
along 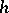 . Choose a simple closed curve
. Choose a simple closed curve 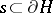 and denote by
and denote by 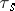 the Dehn twist along
the Dehn twist along  . To be more precise,
. To be more precise, 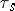 is a homeomorphism
is a homeomorphism 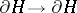 obtained by cutting
obtained by cutting 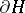 along
along  , isotopically rotating one side of the cut by
, isotopically rotating one side of the cut by 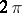 , and gluing back. Let
, and gluing back. Let  . Since
. Since 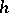 and
and 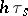 coincide outside a neighbourhood of
coincide outside a neighbourhood of  in
in 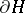 ,
, 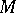 and
and 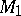 do actually coincide outside regular neighbourhoods of
do actually coincide outside regular neighbourhoods of  in
in 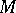 and
and 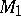 , respectively. It follows that
, respectively. It follows that 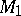 is obtained from
is obtained from 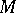 by a Dehn surgery along
by a Dehn surgery along  . One can easily show that the surgery is integer.
. One can easily show that the surgery is integer.
Define a framed link 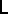 to be a link
to be a link 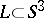 such that every component
such that every component 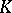 of
of 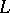 is supplied with an integer number
is supplied with an integer number 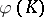 , called a framing. If one performs Dehn surgeries along all components of
, called a framing. If one performs Dehn surgeries along all components of 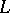 , taking for each component
, taking for each component 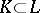 the framing
the framing 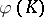 as the parameter
as the parameter  of the surgery, one obtains a
of the surgery, one obtains a  -dimensional manifold
-dimensional manifold 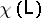 . Since any orientation-preserving homeomorphism of the boundary of a handle-body is isotopic to a product of Dehn twists [a1], it follows from the above relation between Dehn twists and integer Dehn surgeries that for every closed orientable
. Since any orientation-preserving homeomorphism of the boundary of a handle-body is isotopic to a product of Dehn twists [a1], it follows from the above relation between Dehn twists and integer Dehn surgeries that for every closed orientable  -dimensional manifold
-dimensional manifold 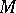 there exists a framed link
there exists a framed link 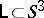 such that
such that 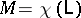 .
.
The following question naturally arises: When do two framed links determine homeomorphic  -dimensional manifolds? In 1978 R. Kirby answered this question by showing that
-dimensional manifolds? In 1978 R. Kirby answered this question by showing that 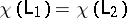 if and only if one can pass from
if and only if one can pass from  to
to 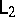 by a sequence of the following moves and their inverses [a2]:
by a sequence of the following moves and their inverses [a2]:
1) replace 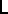 by the link
by the link 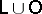 , where
, where  is a new unknotted component with framing
is a new unknotted component with framing 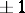 such that
such that  is contained in a
is contained in a  -dimensional ball
-dimensional ball 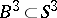 ,
, 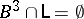 ;
;
2) replace a component 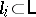 by a geometric sum
by a geometric sum 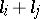 ,
, 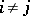 , of
, of 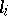 with another component
with another component 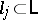 (see [a2] for the exact definition of the geometric sum).
(see [a2] for the exact definition of the geometric sum).
This result became broadly known as the Kirby calculus for framed links, thanks to its convenience for presenting  -dimensional manifolds.
-dimensional manifolds.
Recall that a framing of a knot 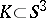 determines a homeomorphism
determines a homeomorphism 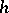 of the standard solid torus
of the standard solid torus  onto a regular neighbourhood
onto a regular neighbourhood  of
of 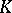 . Denote by
. Denote by 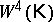 the
the 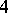 -dimensional manifold
-dimensional manifold 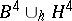 obtained by attaching a
obtained by attaching a 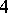 -dimensional handle
-dimensional handle 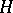 of index
of index  to the
to the 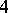 -dimensional ball via the homeomorphism
-dimensional ball via the homeomorphism 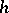 between
between 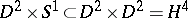 and
and 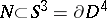 . It follows from the definition that
. It follows from the definition that 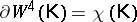 . Similarly, for any framed link
. Similarly, for any framed link 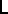 the
the  -dimensional manifold
-dimensional manifold 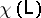 is the boundary of the
is the boundary of the 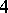 -dimensional manifold
-dimensional manifold 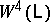 obtained by attaching handles of index
obtained by attaching handles of index  to the
to the 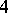 -dimensional ball. Move 1) on
-dimensional ball. Move 1) on 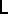 corresponds to replacing
corresponds to replacing 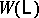 by a connected sum of
by a connected sum of 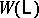 with
with 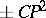 . Move 2) corresponds to a sliding of one handle of index
. Move 2) corresponds to a sliding of one handle of index  over another and does not change
over another and does not change 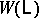 . One can show that any framed link in
. One can show that any framed link in 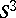 can be transformed by moves 1), 2) and their inverses to a link with even framings [a3]. In the latter case the tangent bundle of the corresponding
can be transformed by moves 1), 2) and their inverses to a link with even framings [a3]. In the latter case the tangent bundle of the corresponding 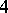 -dimensional manifold is trivial.
-dimensional manifold is trivial.
See [a4] for more details.
References
| [a1] | W.B.R. Lickorish, "A representation of orientable combinatorial 3-manifolds" Ann. Math , 76 (1962) pp. 531–540 |
| [a2] | R. Kirby, "A calculus for framed links in 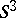 " Invent. Math. , 45 (1978) pp. 35–56 " Invent. Math. , 45 (1978) pp. 35–56 |
| [a3] | S. Kaplan, "Constructing framed 4-manifolds with given almost framed boundaries" Trans. Amer. Math. Soc. , 254 (1979) pp. 237–263 |
| [a4] | A.T. Fomenko, S.V. Matveev, "Algorithmic and computer methods in three dimensional topology" , Kluwer Acad. Publ. (1997) |
Dehn surgery. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dehn_surgery&oldid=46620