Deformation, isometric
of a submanifold 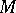 in a Riemannian space
in a Riemannian space 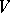
A deformation under which the lengths of curves in 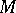 are unchanged. The problem of isometric deformation of surfaces originated with C.F. Gauss, and is a fundamental problem in differential geometry.
are unchanged. The problem of isometric deformation of surfaces originated with C.F. Gauss, and is a fundamental problem in differential geometry.
Apart from the general case, isometric deformations of surfaces preserving some external characteristic have been fairly thoroughly investigated; it usually turned out that only surfaces of a definite class allow of such deformations. Such are, for example: 1) surfaces where the mean curvature is preserved under isometric deformation (surfaces of constant mean curvature, and, in particular, minimal surfaces and some surfaces applicable on a surface of revolution); 2) surfaces where some family of asymptotic lines is preserved under isometric deformation (the ruled surfaces (cf. Ruled surface) are comprised in this class); 3) surfaces allowing a deformation over a principal base; etc.
In character, the problem of isometric deformation of surfaces in Euclidean space can be divided conventionally into that of local isometric deformation, that is, deformation of some small neighbourhood 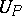 of a point
of a point 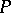 in the surface, and global isometric deformation, that is, deformation of a pre-given piece of the surface or of the whole of it. As a rule, every surface allows of local isometric deformation; however, if
in the surface, and global isometric deformation, that is, deformation of a pre-given piece of the surface or of the whole of it. As a rule, every surface allows of local isometric deformation; however, if  is a flat point, then under certain conditions and with strong regularity assumptions on the allowed deformation,
is a flat point, then under certain conditions and with strong regularity assumptions on the allowed deformation, 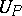 turns out not to have an isometric deformation, even locally.
turns out not to have an isometric deformation, even locally.
The first assertions on global isometric deformation were a theorem of E. Liebmann on the non-isometric deformability of the sphere, and also the following result of D. Hilbert: The maximum principal curvature radius of part of a surface of constant curvature 1 is attained on the boundary. In later investigations it was established that every closed convex surface is not isometrically deformable in the class of convex surfaces without additional regularity conditions. Theorems were discovered of maximum-principle type, relating to isometric deformations of an arbitrary piece of a convex surface of class 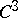 , which imply that a closed convex surface is not isometrically deformable. However, it was proved that a sphere of class
, which imply that a closed convex surface is not isometrically deformable. However, it was proved that a sphere of class 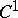 has an isometric deformation in the same class.
has an isometric deformation in the same class.
Only partial results have been established concerning isometric deformation of closed surfaces of positive genus; for example, surfaces of type 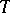 (tori), that is, surfaces consisting of a finite number of regions with piecewise-smooth boundaries in each of which the Gaussian curvature
(tori), that is, surfaces consisting of a finite number of regions with piecewise-smooth boundaries in each of which the Gaussian curvature 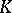 does not change sign and vanishes only on the boundary, and the total curvature of all the regions with
does not change sign and vanishes only on the boundary, and the total curvature of all the regions with 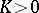 is
is 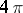 , are not isometrically deformable under certain additional assumptions (analyticity, absence of two closed asymptotic lines); in particular, the ordinary torus is not isometrically deformable.
, are not isometrically deformable under certain additional assumptions (analyticity, absence of two closed asymptotic lines); in particular, the ordinary torus is not isometrically deformable.
Complete non-closed surfaces are usually isometrically deformable. A complete convex surface 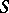 is not isometrically deformable if
is not isometrically deformable if 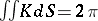 , and is isometrically deformable if
, and is isometrically deformable if 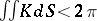 ; every admissible isometric deformation of it is determined by an isometric deformation of its limiting cone. Certain classes of complete surfaces of negative curvature also allow of an isometric deformation; for example, minimal surfaces, in particular a catenoid, can be isometrically deformed into a helicoid.
; every admissible isometric deformation of it is determined by an isometric deformation of its limiting cone. Certain classes of complete surfaces of negative curvature also allow of an isometric deformation; for example, minimal surfaces, in particular a catenoid, can be isometrically deformed into a helicoid.
The study of isometric deformations of non-closed surfaces with boundary also relates mainly to surfaces with Gaussian curvature of constant sign, and the case where the isometric deformation is determined uniquely by different kinds of boundary conditions has been studied in detail. Thus, for any isometric deformation of a closed surface 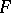 , at least one point of its boundary
, at least one point of its boundary 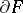 changes its distance from a fixed point
changes its distance from a fixed point 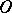 from which
from which 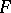 is viewed outwards and which is situated outside the convex hull (so that
is viewed outwards and which is situated outside the convex hull (so that 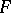 is not isometrically deformable if the distance of an arbitrary point of
is not isometrically deformable if the distance of an arbitrary point of 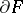 from
from 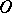 is fixed); likewise, for any isometric deformation of a convex surface
is fixed); likewise, for any isometric deformation of a convex surface 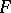 that is uniquely projectable onto a plane
that is uniquely projectable onto a plane 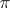 and bounded by a plane contour, at least one point of
and bounded by a plane contour, at least one point of 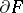 changes its distance from
changes its distance from 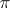 (so that
(so that 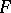 has no sliding isometric deformation, that is, an isometric deformation in which the points of the boundary move parallel to some plane
has no sliding isometric deformation, that is, an isometric deformation in which the points of the boundary move parallel to some plane 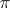 ); for an isometric deformation of a surface of this type, the curvature
); for an isometric deformation of a surface of this type, the curvature 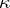 of
of 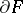 changes for at least one point, and the number of alterations of sign of the difference of the curvatures on the boundaries of
changes for at least one point, and the number of alterations of sign of the difference of the curvatures on the boundaries of 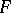 and its deformation
and its deformation  is not less than four (so that if the curvature of the boundary is fixed,
is not less than four (so that if the curvature of the boundary is fixed, 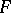 is not isometrically deformable). Concerning surfaces of negative curvature, a fairly wide class of isometric deformations of them are obtained from solutions of the Cauchy problem for the equations of Gauss and Peterson–Codazzi; for example, the isometric deformation of the piece of a surface with
is not isometrically deformable). Concerning surfaces of negative curvature, a fairly wide class of isometric deformations of them are obtained from solutions of the Cauchy problem for the equations of Gauss and Peterson–Codazzi; for example, the isometric deformation of the piece of a surface with 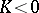 bounded by segments
bounded by segments 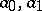 of geodesics and two segments
of geodesics and two segments 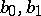 of their orthogonal trajectories is uniquely determined by the isometric deformation of the boundary of
of their orthogonal trajectories is uniquely determined by the isometric deformation of the boundary of 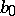 . As for isometric deformations of surfaces with curvature of changing sign, results have been obtained only for the surfaces of revolution.
. As for isometric deformations of surfaces with curvature of changing sign, results have been obtained only for the surfaces of revolution.
In the study of isometric deformation of surfaces, methods of the theory of partial differential equations are applied; for example, equations of elliptic type, which define isometric deformations of surfaces of positive Gaussian curvature, and also of surfaces for which the mean curvature is preserved; moreover, for convex surfaces, a special part is played by the method of direct limit transition of sequences of polytopes (see Glueing method) in combination with theorems on the regularity of a surface having a regular metric. When the convex surface 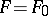 is sufficiently close to its isometric deformation
is sufficiently close to its isometric deformation 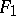 , then the investigation of isometric deformations can be reduced by using a Cohn-Vossen transformation to analogous problems in the theory of infinitesimal deformations (cf. Infinitesimal deformation) of the so-called mean surface
, then the investigation of isometric deformations can be reduced by using a Cohn-Vossen transformation to analogous problems in the theory of infinitesimal deformations (cf. Infinitesimal deformation) of the so-called mean surface
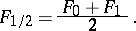 |
References
| [1] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 2 , Moscow-Leningrad (1948) (In Russian) |
| [2] | V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian) |
| [3] | N.V. Efimov, "Qualitative problems of the "local" deformation of surfaces" Trudy Mat. Inst. Steklov. , 30 (1949) (In Russian) |
| [4] | N.V. Efimov, "Qualitative problems of the theory of deformation of surfaces" Uspekhi Mat. Nauk , 2 : 3 (1948) pp. 47–158 (In Russian) |
| [5] | A.V. Pogorelov, "Die Verbiegung konvexer Flächen" , Akademie Verlag (1957) (Translated from Russian) |
| [6] | W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Elementare Differentialgeometrie" , 1 , Springer (1921) |
| [7] | S.E. Cohn-Vossen, "Some problems of differential geometry in the large" , Moscow (1959) (In Russian) |
Comments
An (isometric) deformation of a (piece of a) surface is also known as a bending. An infinitesimal bending is thus an infinitesimal deformation of a surface under which the lengths of curves on the surface is stationary. The velocity field of the deformation is called the bending field. A bending field is trivial if it is the velocity field of a rigid motion of the surface (imbedded in 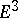 ). A rigid surface is one which admits no non-trivial infinitesimal bendings. A closed regular surface of positive Gaussian curvature is rigid (Blaschke's theorem). Cf. [5], Chapt. 4 for a great deal of material on infinitesimal bendings and rigidity.
). A rigid surface is one which admits no non-trivial infinitesimal bendings. A closed regular surface of positive Gaussian curvature is rigid (Blaschke's theorem). Cf. [5], Chapt. 4 for a great deal of material on infinitesimal bendings and rigidity.
Hilbert's theorem on the maximal principal curvature radius mentioned above can be found in [a6]. It follows readily that the sphere is the only closed (singularity-free) surface of constant positive curvature, a result first proved by H. Liebmann.
References
| [a1] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) |
| [a2] | H. Huck, R. Roitzsch, U. Simon, W. Vortisch, R. Walden, B. Wegner, W. Wendland, "Beweismethoden der Differentialgeometrie im Grossen" , Lect. notes in math. , 335 , Springer (1973) |
| [a3] | N.W. [N.V. Efimov] Efimow, "Flachenverbiegung im Grössen" , Akademie Verlag (1957) (Translated from Russian) |
| [a4] | L. Bianchi, "Vorlesungen über Differentialgeometrie" , Teubner (1910) (Translated from Italian) |
| [a5] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1–4 , Chelsea, reprint (1972) |
| [a6] | D. Hilbert, "Ueber Flächen von konstanter Gausscher Krümmung" Trans. Amer. Math. Soc. , 2 (1901) pp. 87–99 |
Deformation, isometric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Deformation,_isometric&oldid=16801