Darboux theorem
From Encyclopedia of Mathematics
If a real-valued function has a finite derivative at each point of an interval on the real axis, then, if the derivative assumes any two values on this interval, this derivative also assumes all the intermediate values on it.
Comments
This is a kind of intermediate value theorem (for the derivative rather than the function). The following theorem holds for functions themselves: If 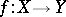 is a continuous mapping between metric spaces, and if
is a continuous mapping between metric spaces, and if  is a connected set, then
is a connected set, then  is connected. (See, e.g., [a1].)
is connected. (See, e.g., [a1].)
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
How to Cite This Entry:
Darboux theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_theorem&oldid=12655
Darboux theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_theorem&oldid=12655
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article