Cubic residue

modulo

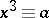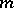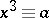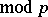An integer for which the congruence () is solvable. If the congruence has no solution, is called a cubic non-residue modulo . If the modulus is a prime number , the congruence () may be checked for solvability using Euler's criterion: The congruence 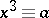(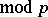), , 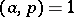is solvable if and only if

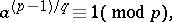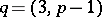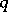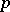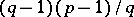where . When the condition is satisfied, the congruence has exactly distinct solutions modulo . It follows from the criterion, in particular, that for a prime number , the sequence of numbers contains exactly cubic non-residues and 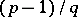cubic residues modulo .

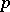Comments

From class field theory one obtains, e.g., that is a cubic residue modulo a prime number 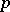if and only if 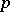can be written in the form 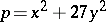with integers and . See also Quadratic residue; Reciprocity laws; Complete system of residues; Reduced system of residues.