Croke isoperimetric inequality

Let be a bounded domain in a complete Riemannian manifold 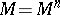with smooth boundary 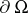. A unit vector 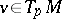is said to be a direction of visibility at 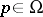if the arc of the geodesic ray 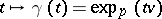from 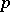up to the first boundary point 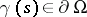is the shortest connection between the points 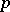and 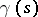, i.e. 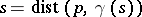. Let 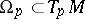be the set of directions of visibility at 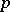and define the minimum visibility angle of by

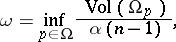where .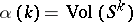

Then the following inequalities hold:

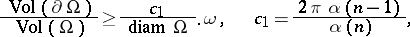(a1)

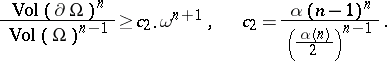(a2)

Both inequalities (a1) and (a2) are sharp in the sense that equality holds if and only if 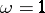and is a hemi-sphere of a sphere of constant positive curvature.

In the proof of the second inequality, special versions of the Berger inequality and the Kazdan inequality are used.

References

[a1]	I. Chavel, "Riemannian geometry: A modern introduction" , Cambridge Univ. Press (1995)
[a2]	C.B. Croke, "Some isoperimetric inequalities and eigenvalue estimates" Ann. Sci. Ecole Norm. Sup. , 13 (1980) pp. 419–435