Continuous flow
A continuous flow in ergodic theory is a family  (where
(where  ranges over the real axis
ranges over the real axis  ) of automorphisms modulo 0 of a measure space
) of automorphisms modulo 0 of a measure space  such that: a)
such that: a)  for any
for any  and all
and all  , except possibly for a set of
, except possibly for a set of  belonging to an exceptional set of measure 0 (which may depend on
belonging to an exceptional set of measure 0 (which may depend on  and
and  ); in other words,
); in other words, 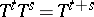
 ; b) for each measurable set
; b) for each measurable set 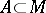 the measure of the symmetric difference
the measure of the symmetric difference 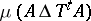 depends continuously on
depends continuously on 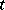 . Let
. Let  be the set of all automorphisms modulo 0 of the space
be the set of all automorphisms modulo 0 of the space  with the usual identification: if
with the usual identification: if 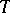 and
and 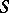 coincide almost-everywhere, then they determine the same element of
coincide almost-everywhere, then they determine the same element of 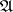 . If
. If  is endowed with the weak topology (see ), then b) means that the mapping
is endowed with the weak topology (see ), then b) means that the mapping 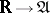 that takes
that takes 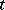 to
to  is continuous.
is continuous.
If 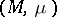 is a Lebesgue space, then the concept of a continuous flow is practically the same as that of a measurable flow: The latter is always a continuous flow (see ), and for any continuous flow
is a Lebesgue space, then the concept of a continuous flow is practically the same as that of a measurable flow: The latter is always a continuous flow (see ), and for any continuous flow 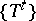 there is a measurable flow
there is a measurable flow 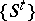 such that
such that 
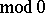 for all
for all 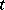 (see ; a related result is proved in , but see also the correction in ). The converse to any of these results depends on the character of the problem in question and the methods used.
(see ; a related result is proved in , but see also the correction in ). The converse to any of these results depends on the character of the problem in question and the methods used.
In another sense the term "continuous flow" can be used to emphasize that the flow is considered in the context of topological dynamics. In this meaning a continuous flow is a collection of homeomorphisms  of a topological space
of a topological space  such that
such that  for all
for all 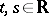 and
and 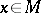 ; the mapping
; the mapping 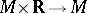 taking
taking 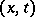 to
to  is continuous.
is continuous.
To avoid confusion with 1) it is better to talk in this case of a topological flow and in the case of 1) of a metric continuity.
References
| [1] | P.R. Halmos, "Lectures on ergodic theory" , Math. Soc. Japan (1956) |
| [2] | E. Hopf, "Ergodentheorie" , Springer (1970) |
| [3] | A.M. Vershik, "Measurable realization of continuous automorphism groups of a unitary ring" Izv. Akad. Nauk. SSSR Ser. Mat. , 29 : 1 (1965) pp. 127–136 |
| [4] | G.W. Mackey, "Point realizations of transformation groups" Illinois J. Math. , 6 : 2 (1962) pp. 327–335 |
| [5] | A. Ramsay, "Virtual groups and group actions" Advances in Math. , 6 : 3 (1971) pp. 253–322 |
Continuous flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_flow&oldid=15434