Continuity, modulus of
One of the basic characteristics of continuous functions. The modulus of continuity of a continuous function 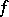 on a closed interval is defined, with
on a closed interval is defined, with 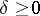 , as
, as
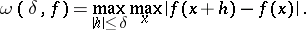 |
The definition of the modulus of continuity was introduced by H. Lebesgue in 1910, although in essence the concept was known earlier. If the modulus of continuity of a function 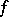 satisfies the condition
satisfies the condition
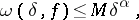 |
where 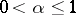 , then
, then  is said to satisfy a Lipschitz condition of order
is said to satisfy a Lipschitz condition of order 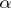 .
.
For a non-negative function  defined for
defined for 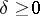 to be the modulus of continuity of some continuous function it is necessary and sufficient that it has the following properties:
to be the modulus of continuity of some continuous function it is necessary and sufficient that it has the following properties: 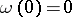 ,
, 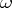 is non-decreasing,
is non-decreasing, 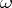 is continuous, and
is continuous, and
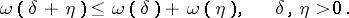 |
One can also consider moduli of continuity of higher orders,
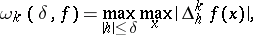 |
where
 |
is the finite difference of order 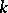 of
of 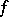 , and moduli of continuity in arbitrary function spaces, for example, the integral modulus of continuity of a function
, and moduli of continuity in arbitrary function spaces, for example, the integral modulus of continuity of a function  that is integrable on
that is integrable on  to the
to the 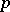 -th power,
-th power, 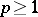 :
:
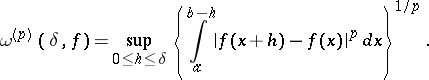 | (*) |
For a 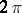 -periodic function the integral in (*) is taken over
-periodic function the integral in (*) is taken over 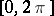 .
.
References
| [1] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
| [2] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
| [3] | V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian) |
Comments
See also Smoothness, modulus of. Moduli of continuity and smoothness are extensively used in approximation theory and Fourier analysis (cf. Harmonic analysis).
Continuity, modulus of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuity,_modulus_of&oldid=16325