Difference between revisions of "Congruence"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex done) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| − | + | {{MSC|11A07}} | |
| − | + | A relation between two integers $ a $ | |
| + | and $ b $ | ||
| + | of the form $ a = b + mk $, | ||
| + | signifying that the difference $ a-b $ | ||
| + | between them is divisible by a given positive integer $ m $, | ||
| + | which is called the modulus (or module) of the congruence; $ a $ | ||
| + | is then called a remainder of $ b $ | ||
| + | modulo $ m $( | ||
| + | cf. [[Remainder of an integer|Remainder of an integer]]). In order to express the congruence of the numbers $ a $ | ||
| + | and $ b $ | ||
| + | modulo $ m $, | ||
| + | the symbol | ||
| − | + | $$ | |
| + | a \ \equiv \ b \ ( \mathop{\rm mod}\nolimits \ m) | ||
| + | $$ | ||
| − | is used. | + | is used. If the difference $ a-b $ |
| + | is not divisible by $ m $, | ||
| + | then $ a $ | ||
| + | and $ b $ | ||
| + | are said to be incongruent modulo $ m $, | ||
| + | and in order to express the incongruency of $ a $ | ||
| + | and $ b $, | ||
| + | the symbol | ||
| − | Congruence modulo a fixed | + | $$ |
| + | a \ \not\equiv \ b \ ( \mathop{\rm mod}\nolimits \ m) | ||
| + | $$ | ||
| + | |||
| + | is used. The congruence $ a \equiv b \ ( \mathop{\rm mod}\nolimits \ m) $ | ||
| + | expresses that $ a $ | ||
| + | and $ b $ | ||
| + | have identical remainders when divided by $ m $. | ||
| + | |||
| + | Congruence modulo a fixed $ m $ | ||
| + | is an [[equivalence relation]]: it is reflexive, since $ a \equiv a $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $); | ||
| + | symmetric, since it follows from $ a \equiv b $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $) | ||
| + | that $ b \equiv a $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $); | ||
| + | and transitive, since it follows from $ a \equiv b $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $) | ||
| + | and $ b \equiv c $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $) | ||
| + | that $ a \equiv c $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $). | ||
| + | Therefore, the relation " (modm)" divides the set of all integers into non-intersecting equivalence classes $ A,\ B ,\dots $. | ||
| + | Two integers belong to one and the same class if and only if they are congruent modulo $ m $. | ||
| + | These classes are called residue classes modulo $ m $. | ||
| + | Every integer is congruent modulo $ m $ | ||
| + | with just one of the numbers $ 0 \dots m-1 $; | ||
| + | the numbers $ 0 \dots m-1 $ | ||
| + | belong to different classes, so that there are exactly $ m $ | ||
| + | residue classes, while the numbers $ 0 \dots m-1 $ | ||
| + | form a set of representatives of these classes. Any set of $ m $ | ||
| + | integers containing one number from each residue class is called a complete residue system modulo $ m $. | ||
Congruences modulo one and the same number can be added, subtracted and multiplied in the same way as normal equalities, i.e. it follows from | Congruences modulo one and the same number can be added, subtracted and multiplied in the same way as normal equalities, i.e. it follows from | ||
| − | + | $$ | |
| + | a \ \equiv \ b \ ( \mathop{\rm mod}\nolimits \ m) \ \ | ||
| + | \textrm{ and } \ \ c \ \equiv \ d \ ( \mathop{\rm mod}\nolimits \ m) | ||
| + | $$ | ||
that | that | ||
| − | + | $$ | |
| + | a \pm c \ \equiv \ b \pm d \ ( \mathop{\rm mod}\nolimits \ m) \ \ | ||
| + | \textrm{ and } \ \ | ||
| + | ac \ \equiv \ bd \ ( \mathop{\rm mod}\nolimits \ m). | ||
| + | $$ | ||
| − | Both parts of a congruence can be multiplied by one and the same integer, and both can be divided by a common divisor, as long as the divisor is relatively prime with the modulus of the congruence. If a common divisor of a number by which both parts of the congruence are divisible and the modulus | + | Both parts of a congruence can be multiplied by one and the same integer, and both can be divided by a common divisor, as long as the divisor is relatively prime with the modulus of the congruence. If a common divisor of a number by which both parts of the congruence are divisible and the modulus $ m $ |
| + | of the congruence is $ d $, | ||
| + | then after dividing by $ d $ | ||
| + | a congruence modulo $ m/d $ | ||
| + | is obtained. | ||
| − | The operations of addition, subtraction and multiplication of congruences induce similar operations on the residue classes. Thus, if | + | The operations of addition, subtraction and multiplication of congruences induce similar operations on the residue classes. Thus, if $ a $ |
| + | and $ b $ | ||
| + | are arbitrary elements from the residue classes $ A $ | ||
| + | and $ B $, | ||
| + | respectively, then $ a+b $ | ||
| + | always belongs to one and the same residue class, called the sum $ A+B $ | ||
| + | of the classes $ A $ | ||
| + | and $ B $. | ||
| + | The difference $ A-B $ | ||
| + | and the product $ A \cdot B $ | ||
| + | of the two residue classes $ A $ | ||
| + | and $ B $ | ||
| + | are defined in the same way. The residue classes modulo $ m $ | ||
| + | form an Abelian group of order $ m $ | ||
| + | with respect to addition. The zero element of this group is the class consisting of all integers that are multiples of the number $ m $; | ||
| + | the negative (inverse) of a class $ A $ | ||
| + | is the class consisting of all elements of $ A $ | ||
| + | with a minus sign. Moreover, the residue classes modulo $ m $ | ||
| + | form a ring relative to the above-defined operations of addition, subtraction and multiplication. | ||
| − | Let | + | Let $ F(x _{1} \dots x _{n} ) $ |
| + | be a polynomial in $ n $ | ||
| + | variables with integer coefficients. An equation of the form | ||
| − | + | $$ \tag{*} | |
| + | F(x _{1} \dots x _{n} ) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ m) | ||
| + | $$ | ||
| − | is called a [[Congruence equation|congruence equation]]. A solution of the congruence (*) is any set | + | is called a [[Congruence equation|congruence equation]]. A solution of the congruence (*) is any set $ a _{1} \dots a _{n} $ |
| + | of integer values of the unknowns $ x _{1} \dots x _{n} $ | ||
| + | such that the number $ F(a _{1} \dots a _{n} ) $ | ||
| + | is congruent to zero modulo $ m $. | ||
| + | If $ a _{i} $, | ||
| + | $ 1 \leq i \leq n $, | ||
| + | belong to the residue classes $ X _{i} $ | ||
| + | modulo $ m $, | ||
| + | then any other set $ a _ i^ \prime \in X _{i} $, | ||
| + | $ 1 \leq i \leq n $, | ||
| + | is also a solution of the congruence. One therefore calls the set of residue classes itself, of which $ a _{1} \dots a _{n} $ | ||
| + | are representatives, a solution of the congruence (*), i.e. a solution of the algebraic equation $ F(x _{1} \dots x _{n} ) = 0 $ | ||
| + | in the ring of residue classes modulo $ m $. | ||
| + | Given this manner of speaking, the congruence (*) has as many solutions as there are sets of residue classes of a complete system modulo $ m $ | ||
| + | that satisfy the equation $ F(x _{1} \dots x _{n} ) = 0 $. | ||
| + | The number of solutions of more general forms of congruences, as well as of systems of congruences, is defined in the same way. | ||
A congruence of the first degree | A congruence of the first degree | ||
| − | + | $$ | |
| + | ax \ \equiv \ b \ ( \mathop{\rm mod}\nolimits \ m), | ||
| + | $$ | ||
| − | where | + | where $ a $ |
| + | is relatively prime with $ m $( | ||
| + | this is denoted by $ (a,\ m) = 1 $), | ||
| + | has a unique solution. Those residue classes modulo $ m $ | ||
| + | whose elements are relatively prime with $ m $ | ||
| + | form an Abelian group with respect to multiplication. The unit of this group is the class $ E $ | ||
| + | which contains the number 1, while the inverse of a class $ A $ | ||
| + | is the class $ A^{-1} $ | ||
| + | that contains the solutions of the congruence | ||
| − | + | $$ | |
| + | ax \ \equiv \ 1 \ ( \mathop{\rm mod}\nolimits \ m),\ \ \textrm{ where } \ a \in A. | ||
| + | $$ | ||
| − | The residue classes modulo | + | The residue classes modulo $ m $ |
| + | consisting of elements which are relatively prime with $ m $ | ||
| + | are called reduced classes, while any system of numbers containing one number from each reduced class is called a reduced residue system. A reduced residue system consists of $ \phi (m) $ | ||
| + | elements, where $ \phi (m) $ | ||
| + | is the [[Euler function|Euler function]], which is equal to the number of elements in the set $ 1 \dots m $ | ||
| + | that are relatively prime with $ m $. | ||
| − | The structure of the multiplicative group of reduced residue classes modulo | + | The structure of the multiplicative group of reduced residue classes modulo $ m $ |
| + | is explained to a significant degree by the theorems of L. Euler and P. Fermat, which show that the order of any element of the group divides $ \phi (m) $. | ||
| − | Euler's theorem. If | + | Euler's theorem. If $ a $ |
| + | and $ m $ | ||
| + | are relatively prime, then | ||
| − | + | $$ | |
| + | a ^ {\phi (m)} \ \equiv \ 1 \ ( \mathop{\rm mod}\nolimits \ m) | ||
| + | $$ | ||
(see [[Euler theorem|Euler theorem]]). | (see [[Euler theorem|Euler theorem]]). | ||
| − | The particular case of this theorem for a prime modulus is Fermat's theorem: If | + | The particular case of this theorem for a prime modulus is Fermat's theorem: If $ p $ |
| + | is a prime number and $ a $ | ||
| + | is not divisible by $ p $, | ||
| + | then | ||
| − | + | $$ | |
| + | a^{p-1} \ \equiv \ 1 \ ( \mathop{\rm mod}\nolimits \ p) | ||
| + | $$ | ||
(see [[Fermat little theorem|Fermat little theorem]]). | (see [[Fermat little theorem|Fermat little theorem]]). | ||
| − | An important concept in the study of the multiplicative group of reduced residue classes is the concept of a [[Primitive root|primitive root]] modulo | + | An important concept in the study of the multiplicative group of reduced residue classes is the concept of a [[Primitive root|primitive root]] modulo $ m $. |
| + | When $ (a,\ m) = 1 $, | ||
| + | there exists a positive integer $ \gamma $ | ||
| + | for which $ a^ \gamma \equiv 1 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $), | ||
| + | for example $ \gamma = \phi (m) $. | ||
| + | The least of these is called the index to which the $ number $ | ||
| + | $ a $ | ||
| + | modulo $ m $ | ||
| + | belongs. | ||
| − | Numbers which belong to the index | + | Numbers which belong to the index $ \phi (m) $( |
| + | if there are any) are called primitive roots modulo $ m $. | ||
| + | If $ g $ | ||
| + | is a primitive root modulo $ m $ | ||
| + | and $ \gamma $ | ||
| + | runs through a complete residue system modulo $ \phi (m) $, | ||
| + | then $ g^ \gamma $ | ||
| + | runs through a reduced residue system modulo $ m $. | ||
| + | Thus, if $ (a,\ m) = 1 $, | ||
| + | then for a certain $ \gamma $ | ||
| + | from the set $ 0 \dots \phi (m)-1 $, | ||
| + | the congruence $ a \equiv g^ \gamma $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $) | ||
| + | holds. This $ \gamma $ | ||
| + | is called the index of the number $ a $ | ||
| + | modulo $ m $ | ||
| + | with respect to the basis $ g $ | ||
| + | and is denoted by the symbol $ \mathop{\rm ind}\nolimits \ a $ | ||
| + | or, more precisely, $ \mathop{\rm ind}\nolimits _{g} \ a $. | ||
| + | The properties of an index are broadly the same as the properties of a logarithm. Primitive roots exist only for moduli $ m > 1 $ | ||
| + | of the form $ 2,\ 4,\ p^ \alpha ,\ 2p^ \alpha $, | ||
| + | where $ p \geq 3 $ | ||
| + | is a prime number and $ \alpha \geq 1 $ | ||
| + | is an integer. In these cases, the multiplicative group of reduced residue classes modulo $ m $ | ||
| + | is simply the cyclic group of order $ \phi (m) $. | ||
| + | In the other cases, the groups of reduced residue classes have a much more complex structure. | ||
| − | Many problems in number theory reduce to the question of the solvability or unsolvability of some type of congruence. As a result of this, the theory of congruences, which was first systematically developed by C.F. Gauss (see [[#References|[5]]]) and used by him as a foundation of classical number theory, is to this day one of the basic means of solving number-theoretical problems. In this connection, research into the question of the number of solutions of a congruence equation is of fundamental importance to number theory. The simplest types of congruence equations are congruences of the first degree with one unknown | + | Many problems in number theory reduce to the question of the solvability or unsolvability of some type of congruence. As a result of this, the theory of congruences, which was first systematically developed by C.F. Gauss (see [[#References|[5]]]) and used by him as a foundation of classical number theory, is to this day one of the basic means of solving number-theoretical problems. In this connection, research into the question of the number of solutions of a congruence equation is of fundamental importance to number theory. The simplest types of congruence equations are congruences of the first degree with one unknown $ ax \equiv b $( |
| + | $ \mathop{\rm mod}\nolimits \ m $). | ||
| + | A complete answer to the question of the number of solutions of congruences of the first degree is provided by the following theorem. Let $ (a,\ m) = d $. | ||
| + | The congruence $ ax \equiv b $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m $) | ||
| + | is unsolvable if $ b $ | ||
| + | is not divisible by $ d $. | ||
| + | When $ b $ | ||
| + | is a multiple of $ d $, | ||
| + | the congruence has precisely $ d $ | ||
| + | solutions. | ||
The question of the solvability of a system of linear congruences | The question of the solvability of a system of linear congruences | ||
| − | + | $$ | |
| + | \sum _ { j=1 } ^ s a _{ij} x _{j} \ \equiv \ b _{i} \ ( \mathop{\rm mod}\nolimits \ p),\ \ | ||
| + | i = 1 \dots t, | ||
| + | $$ | ||
| − | modulo a prime number | + | modulo a prime number $ p > 2 $ |
| + | is solved completely in the general theory of linear equations over arbitrary fields. The case of a composite modulus can be reduced to the case of a prime modulus. | ||
The form of algebraic congruences with one unknown which is the next most complex to study is a [[Two-term congruence|two-term congruence]] | The form of algebraic congruences with one unknown which is the next most complex to study is a [[Two-term congruence|two-term congruence]] | ||
| − | + | $$ | |
| + | x^{n} \ \equiv \ a \ ( \mathop{\rm mod}\nolimits \ m) \ \ \textrm{ when } \ (a,\ m) = 1. | ||
| + | $$ | ||
| − | If the congruence | + | If the congruence $ x^{n} \equiv a \ ( \mathop{\rm mod}\nolimits \ m) $ |
| + | has solutions, then $ a $ | ||
| + | is called an $ n $- | ||
| + | th power residue modulo $ m $; | ||
| + | if it does not, then $ a $ | ||
| + | is called an $ n $- | ||
| + | th power non-residue modulo $ m $. | ||
| + | More specifically, when $ n=2 $, | ||
| + | the residues or non-residues are called quadratic, when $ n=3 $, | ||
| + | cubic, and when $ n=4 $, | ||
| + | bi-quadratic. | ||
The question of the number of solutions of a congruence | The question of the number of solutions of a congruence | ||
| − | + | $$ | |
| + | f(x) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ m) | ||
| + | $$ | ||
| − | modulo a composite number | + | modulo a composite number $ m = p _{1} ^ {\alpha _ 1} \dots p _{s} ^ {\alpha _ s} $ |
| + | reduces to the question of the number of solutions of the congruence | ||
| − | + | $$ | |
| + | f(x) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ p _{i} ^ {\alpha _ i} ) | ||
| + | $$ | ||
| − | for every | + | for every $ i = 1 \dots s $. |
| + | The following theorem holds: If $ m _{1} \dots m _{r} $ | ||
| + | are pairwise relatively prime (coprime) positive integers, then the number $ N $ | ||
| + | of solutions of the congruence $ f(x) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m _{1} \dots m _{r} $) | ||
| + | can be expressed by the values $ N _{i} $, | ||
| + | $ i = 1 \dots r $, | ||
| + | which are equal to the number of solutions of the corresponding congruences $ f(x) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ m _{i} $) | ||
| + | according to the formula $ N = \prod _ i=1^{r} N _{i} $. | ||
| + | In its turn, the question of the number of solutions of the congruence | ||
| − | + | $$ | |
| + | f(x) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ p^ \alpha ),\ \ | ||
| + | \alpha > 1 , | ||
| + | $$ | ||
| − | generally reduces to the question of the number of solutions of the congruence | + | generally reduces to the question of the number of solutions of the congruence $ f(x) \equiv 0 $( |
| + | $ \mathop{\rm mod}\nolimits \ p $) | ||
| + | where $ p $ | ||
| + | is a prime number. The following theorem forms the basis of this reduction: Every solution $ x \equiv x _{1} $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $) | ||
| + | of a congruence $ f(x) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $) | ||
| + | can be uniquely continued to a solution $ x \equiv x _ \alpha $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p^ \alpha $) | ||
| + | of the congruence $ f(x) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p^ \alpha $) | ||
| + | provided that the formal derivative $ f ^ {\ \prime} (x _{1} ) \not\equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $), | ||
| + | i.e. a unique solution $ x _ \alpha $ | ||
| + | of the congruence $ f(x) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p^ \alpha $) | ||
| + | then exists such that $ x _ \alpha \equiv x _{1} $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $). | ||
| − | A similar situation also arises in the case of a congruence equation in several variables, i.e. in non-degenerate cases the question of the number of solutions of the congruence | + | A similar situation also arises in the case of a congruence equation in several variables, i.e. in non-degenerate cases the question of the number of solutions of the congruence $ F(x _{1} \dots x _{n} ) = 0 $( |
| + | $ \mathop{\rm mod}\nolimits \ m $), | ||
| + | modulo a composite number $ m $ | ||
| + | reduces to the question of the number of solutions of the same congruence modulo a prime number $ m $. | ||
| − | An upper bound for the number of solutions of a congruence | + | An upper bound for the number of solutions of a congruence $ f(x) \equiv 0 $( |
| + | $ \mathop{\rm mod}\nolimits \ p $), | ||
| + | where $ f(x) = a _{0} x^{n} + \dots + a _{n} $, | ||
| + | $ a _{0} \not\equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $), | ||
| + | is given by Lagrange's theorem: The number of solutions of a congruence $ f(x) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $) | ||
| + | does not exceed the degree of the polynomial $ f(x) $. | ||
| + | The study of the question of the exact number of solutions of the congruence $ f(x) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $) | ||
| + | generally meets with considerable difficulties, so that only a few results have so far (1984) been obtained in this area. | ||
| − | The Lagrange theorem ceases to hold in the case of a composite modulus. The above-mentioned specific property of prime numbers is explained by the fact that the residue classes modulo a prime number | + | The Lagrange theorem ceases to hold in the case of a composite modulus. The above-mentioned specific property of prime numbers is explained by the fact that the residue classes modulo a prime number $ p $ |
| + | form a field (see [[Congruence modulo a prime number|Congruence modulo a prime number]]). Another specific property of prime numbers which is explained by this fact is expressed in the [[Wilson theorem|Wilson theorem]]. | ||
In the study of quadratic congruences | In the study of quadratic congruences | ||
| − | + | $$ | |
| + | x^{2} \ \equiv \ a \ ( \mathop{\rm mod}\nolimits \ p) | ||
| + | $$ | ||
| − | modulo a prime number | + | modulo a prime number $ p $, |
| + | as well as in their applications, the [[Legendre symbol|Legendre symbol]] and the [[Jacobi symbol|Jacobi symbol]] are introduced. | ||
Congruence equations modulo a prime number in two unknowns (and generally in any number of unknowns), | Congruence equations modulo a prime number in two unknowns (and generally in any number of unknowns), | ||
| − | + | $$ | |
| + | F(x,\ y) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ p) , | ||
| + | $$ | ||
| − | can be treated as equations over the finite prime field of | + | can be treated as equations over the finite prime field of $ p $ |
| + | elements. Methods of the theory of algebraic functions and algebraic geometry are therefore used in studying them, as well as methods of number theory. Using these methods, an asymptotic expansion in the form | ||
| − | + | $$ | |
| + | N _{p} \ = \ p + O( \sqrt p ) | ||
| + | $$ | ||
| − | was first obtained for the number | + | was first obtained for the number $ N _{p} $ |
| + | of solutions of a broad class of congruences $ F(x,\ y) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $). | ||
| + | The same asymptotic expansions were subsequently deduced using methods of number theory without going beyond the limits of the theory of congruences (see [[#References|[6]]]). | ||
| − | Comparatively little is known about algebraic congruences in several unknowns. The following can be considered as a general result (Chevalley's theorem). Let | + | Comparatively little is known about algebraic congruences in several unknowns. The following can be considered as a general result (Chevalley's theorem). Let $ F(x _{1} \dots x _{n} ) $ |
| + | be a polynomial with integer rational coefficients, the degree of which is less than $ n $. | ||
| + | The number of solutions of the congruence | ||
| − | + | $$ | |
| + | F(x _{1} \dots x _{n} ) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ p) | ||
| + | $$ | ||
| − | is then divisible by the prime number | + | is then divisible by the prime number $ p $. |
| + | One very strong result for this type of questions was obtained by P. Deligne [[#References|[9]]] (see also [[#References|[10]]]). | ||
| − | Great value is also attached to research into the question of the number of solutions of congruences in an incomplete residue system. A systematic solution to this type of problems was first attempted by I.M. Vinogradov (see [[#References|[4]]]). An example of this type of problems is the problem of the distribution of quadratic residues and non-residues in the set | + | Great value is also attached to research into the question of the number of solutions of congruences in an incomplete residue system. A systematic solution to this type of problems was first attempted by I.M. Vinogradov (see [[#References|[4]]]). An example of this type of problems is the problem of the distribution of quadratic residues and non-residues in the set $ 1 \dots p-1 $, |
| + | which is connected with the study of solutions of the congruence $ y^{2} \equiv x $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p $) | ||
| + | (see [[Vinogradov hypotheses|Vinogradov hypotheses]]; [[Distribution of power residues and non-residues|Distribution of power residues and non-residues]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) {{MR|0195803}} {{ZBL|0145.04902}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.A. Venkov, "Elementary number theory" , Wolters-Noordhoff (1970) (Translated from Russian) {{MR|0265267}} {{ZBL|0204.37101}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.M. Vinogradov, "Fundamentals of number theory" , Moscow (1972) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) {{MR|0807530}} {{ZBL|0577.01049}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> C.F. Gauss, "Untersuchungen über höhere Arithmetik" , Springer (1889) (Translated from Latin) {{MR|0188045}} {{ZBL|21.0166.04}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S.A. Stepanov, "A constructive method in the theory of equations over finite fields" ''Trudy Mat. Inst. Steklov.'' , '''132''' (1973) pp. 237–246 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> H. Hasse, "Zahlentheorie" , Akademie Verlag (1963) {{MR|0153659}} {{ZBL|1038.11500}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> K. Chandrasekharan, "Introduction to analytic number theory" , Springer (1968) {{MR|0249348}} {{ZBL|0169.37502}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> P. Deligne, "La conjecture de Weil I" ''Publ. Math. IHES'' , '''43''' (1974) pp. 273–307 {{MR|0340258}} {{ZBL|0314.14007}} {{ZBL|0287.14001}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> N.M. Katz, "An overview of Deligne's proof of the Riemann hypothesis for varieties over finite fields" F.E. Browder (ed.) , ''Mathematical developments arising from Hilbert problems'' , ''Proc. Symp. Pure Math.'' , '''28''' , Amer. Math. Soc. (1976) pp. 275–305</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) {{MR|0195803}} {{ZBL|0145.04902}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.A. Venkov, "Elementary number theory" , Wolters-Noordhoff (1970) (Translated from Russian) {{MR|0265267}} {{ZBL|0204.37101}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.M. Vinogradov, "Fundamentals of number theory" , Moscow (1972) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) {{MR|0807530}} {{ZBL|0577.01049}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> C.F. Gauss, "Untersuchungen über höhere Arithmetik" , Springer (1889) (Translated from Latin) {{MR|0188045}} {{ZBL|21.0166.04}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S.A. Stepanov, "A constructive method in the theory of equations over finite fields" ''Trudy Mat. Inst. Steklov.'' , '''132''' (1973) pp. 237–246 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> H. Hasse, "Zahlentheorie" , Akademie Verlag (1963) {{MR|0153659}} {{ZBL|1038.11500}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> K. Chandrasekharan, "Introduction to analytic number theory" , Springer (1968) {{MR|0249348}} {{ZBL|0169.37502}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> P. Deligne, "La conjecture de Weil I" ''Publ. Math. IHES'' , '''43''' (1974) pp. 273–307 {{MR|0340258}} {{ZBL|0314.14007}} {{ZBL|0287.14001}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> N.M. Katz, "An overview of Deligne's proof of the Riemann hypothesis for varieties over finite fields" F.E. Browder (ed.) , ''Mathematical developments arising from Hilbert problems'' , ''Proc. Symp. Pure Math.'' , '''28''' , Amer. Math. Soc. (1976) pp. 275–305</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The simultaneous system of congruences | + | The simultaneous system of congruences $ x \equiv c _{i} $( |
| + | $ \mathop{\rm mod}\nolimits \ m _{i} $), | ||
| + | $ i = 1 \dots r $, | ||
| + | where $ ( m _{i} ,\ m _{j} ) = 1 $ | ||
| + | for all $ i \neq j $, | ||
| + | has a unique residue class modulo $ M = m _{1} \dots m _{r} $ | ||
| + | as solution. This is the content of the [[Chinese remainder theorem|Chinese remainder theorem]]. | ||
| − | The procedure to extend solutions of | + | The procedure to extend solutions of $ f (x) \equiv 0 $( |
| + | $ \mathop{\rm mod}\nolimits \ p $) | ||
| + | to solutions of $ f (x) \equiv 0 $( | ||
| + | $ \mathop{\rm mod}\nolimits \ p^ \alpha $) | ||
| + | is described in the [[Hensel lemma|Hensel lemma]] (cf. [[#References|[a2]]]), and extends to a technique in the theory of $ p $- | ||
| + | adic numbers (cf. [[P-adic number| $ p $- | ||
| + | adic number]]). | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. 5; 7; 8 {{MR|0568909}} {{ZBL|0423.10001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Koblitz, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024850/c024850255.png" />-adic numbers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024850/c024850256.png" />-adic analysis and zeta-functions" , Springer (1977) pp. Chapt. 1 {{MR|466081}} {{ZBL|}} </TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. 5; 7; 8 {{MR|0568909}} {{ZBL|0423.10001}} </TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Koblitz, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024850/c024850255.png" />-adic numbers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c024/c024850/c024850256.png" />-adic analysis and zeta-functions" , Springer (1977) pp. Chapt. 1 {{MR|466081}} {{ZBL|}} </TD></TR> | ||
| + | </table> | ||
Revision as of 09:30, 1 February 2020
2020 Mathematics Subject Classification: Primary: 11A07 [MSN][ZBL]
A relation between two integers $ a $ and $ b $ of the form $ a = b + mk $, signifying that the difference $ a-b $ between them is divisible by a given positive integer $ m $, which is called the modulus (or module) of the congruence; $ a $ is then called a remainder of $ b $ modulo $ m $( cf. Remainder of an integer). In order to express the congruence of the numbers $ a $ and $ b $ modulo $ m $, the symbol
$$ a \ \equiv \ b \ ( \mathop{\rm mod}\nolimits \ m) $$
is used. If the difference $ a-b $ is not divisible by $ m $, then $ a $ and $ b $ are said to be incongruent modulo $ m $, and in order to express the incongruency of $ a $ and $ b $, the symbol
$$ a \ \not\equiv \ b \ ( \mathop{\rm mod}\nolimits \ m) $$
is used. The congruence $ a \equiv b \ ( \mathop{\rm mod}\nolimits \ m) $ expresses that $ a $ and $ b $ have identical remainders when divided by $ m $.
Congruence modulo a fixed $ m $ is an equivalence relation: it is reflexive, since $ a \equiv a $( $ \mathop{\rm mod}\nolimits \ m $); symmetric, since it follows from $ a \equiv b $( $ \mathop{\rm mod}\nolimits \ m $) that $ b \equiv a $( $ \mathop{\rm mod}\nolimits \ m $); and transitive, since it follows from $ a \equiv b $( $ \mathop{\rm mod}\nolimits \ m $) and $ b \equiv c $( $ \mathop{\rm mod}\nolimits \ m $) that $ a \equiv c $( $ \mathop{\rm mod}\nolimits \ m $). Therefore, the relation " (modm)" divides the set of all integers into non-intersecting equivalence classes $ A,\ B ,\dots $. Two integers belong to one and the same class if and only if they are congruent modulo $ m $. These classes are called residue classes modulo $ m $. Every integer is congruent modulo $ m $ with just one of the numbers $ 0 \dots m-1 $; the numbers $ 0 \dots m-1 $ belong to different classes, so that there are exactly $ m $ residue classes, while the numbers $ 0 \dots m-1 $ form a set of representatives of these classes. Any set of $ m $ integers containing one number from each residue class is called a complete residue system modulo $ m $.
Congruences modulo one and the same number can be added, subtracted and multiplied in the same way as normal equalities, i.e. it follows from
$$ a \ \equiv \ b \ ( \mathop{\rm mod}\nolimits \ m) \ \ \textrm{ and } \ \ c \ \equiv \ d \ ( \mathop{\rm mod}\nolimits \ m) $$
that
$$ a \pm c \ \equiv \ b \pm d \ ( \mathop{\rm mod}\nolimits \ m) \ \ \textrm{ and } \ \ ac \ \equiv \ bd \ ( \mathop{\rm mod}\nolimits \ m). $$
Both parts of a congruence can be multiplied by one and the same integer, and both can be divided by a common divisor, as long as the divisor is relatively prime with the modulus of the congruence. If a common divisor of a number by which both parts of the congruence are divisible and the modulus $ m $ of the congruence is $ d $, then after dividing by $ d $ a congruence modulo $ m/d $ is obtained.
The operations of addition, subtraction and multiplication of congruences induce similar operations on the residue classes. Thus, if $ a $ and $ b $ are arbitrary elements from the residue classes $ A $ and $ B $, respectively, then $ a+b $ always belongs to one and the same residue class, called the sum $ A+B $ of the classes $ A $ and $ B $. The difference $ A-B $ and the product $ A \cdot B $ of the two residue classes $ A $ and $ B $ are defined in the same way. The residue classes modulo $ m $ form an Abelian group of order $ m $ with respect to addition. The zero element of this group is the class consisting of all integers that are multiples of the number $ m $; the negative (inverse) of a class $ A $ is the class consisting of all elements of $ A $ with a minus sign. Moreover, the residue classes modulo $ m $ form a ring relative to the above-defined operations of addition, subtraction and multiplication.
Let $ F(x _{1} \dots x _{n} ) $ be a polynomial in $ n $ variables with integer coefficients. An equation of the form
$$ \tag{*} F(x _{1} \dots x _{n} ) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ m) $$
is called a congruence equation. A solution of the congruence (*) is any set $ a _{1} \dots a _{n} $ of integer values of the unknowns $ x _{1} \dots x _{n} $ such that the number $ F(a _{1} \dots a _{n} ) $ is congruent to zero modulo $ m $. If $ a _{i} $, $ 1 \leq i \leq n $, belong to the residue classes $ X _{i} $ modulo $ m $, then any other set $ a _ i^ \prime \in X _{i} $, $ 1 \leq i \leq n $, is also a solution of the congruence. One therefore calls the set of residue classes itself, of which $ a _{1} \dots a _{n} $ are representatives, a solution of the congruence (*), i.e. a solution of the algebraic equation $ F(x _{1} \dots x _{n} ) = 0 $ in the ring of residue classes modulo $ m $. Given this manner of speaking, the congruence (*) has as many solutions as there are sets of residue classes of a complete system modulo $ m $ that satisfy the equation $ F(x _{1} \dots x _{n} ) = 0 $. The number of solutions of more general forms of congruences, as well as of systems of congruences, is defined in the same way.
A congruence of the first degree
$$ ax \ \equiv \ b \ ( \mathop{\rm mod}\nolimits \ m), $$
where $ a $ is relatively prime with $ m $( this is denoted by $ (a,\ m) = 1 $), has a unique solution. Those residue classes modulo $ m $ whose elements are relatively prime with $ m $ form an Abelian group with respect to multiplication. The unit of this group is the class $ E $ which contains the number 1, while the inverse of a class $ A $ is the class $ A^{-1} $ that contains the solutions of the congruence
$$ ax \ \equiv \ 1 \ ( \mathop{\rm mod}\nolimits \ m),\ \ \textrm{ where } \ a \in A. $$
The residue classes modulo $ m $ consisting of elements which are relatively prime with $ m $ are called reduced classes, while any system of numbers containing one number from each reduced class is called a reduced residue system. A reduced residue system consists of $ \phi (m) $ elements, where $ \phi (m) $ is the Euler function, which is equal to the number of elements in the set $ 1 \dots m $ that are relatively prime with $ m $.
The structure of the multiplicative group of reduced residue classes modulo $ m $ is explained to a significant degree by the theorems of L. Euler and P. Fermat, which show that the order of any element of the group divides $ \phi (m) $.
Euler's theorem. If $ a $ and $ m $ are relatively prime, then
$$ a ^ {\phi (m)} \ \equiv \ 1 \ ( \mathop{\rm mod}\nolimits \ m) $$
(see Euler theorem).
The particular case of this theorem for a prime modulus is Fermat's theorem: If $ p $ is a prime number and $ a $ is not divisible by $ p $, then
$$ a^{p-1} \ \equiv \ 1 \ ( \mathop{\rm mod}\nolimits \ p) $$
(see Fermat little theorem).
An important concept in the study of the multiplicative group of reduced residue classes is the concept of a primitive root modulo $ m $. When $ (a,\ m) = 1 $, there exists a positive integer $ \gamma $ for which $ a^ \gamma \equiv 1 $( $ \mathop{\rm mod}\nolimits \ m $), for example $ \gamma = \phi (m) $. The least of these is called the index to which the $ number $ $ a $ modulo $ m $ belongs.
Numbers which belong to the index $ \phi (m) $( if there are any) are called primitive roots modulo $ m $. If $ g $ is a primitive root modulo $ m $ and $ \gamma $ runs through a complete residue system modulo $ \phi (m) $, then $ g^ \gamma $ runs through a reduced residue system modulo $ m $. Thus, if $ (a,\ m) = 1 $, then for a certain $ \gamma $ from the set $ 0 \dots \phi (m)-1 $, the congruence $ a \equiv g^ \gamma $( $ \mathop{\rm mod}\nolimits \ m $) holds. This $ \gamma $ is called the index of the number $ a $ modulo $ m $ with respect to the basis $ g $ and is denoted by the symbol $ \mathop{\rm ind}\nolimits \ a $ or, more precisely, $ \mathop{\rm ind}\nolimits _{g} \ a $. The properties of an index are broadly the same as the properties of a logarithm. Primitive roots exist only for moduli $ m > 1 $ of the form $ 2,\ 4,\ p^ \alpha ,\ 2p^ \alpha $, where $ p \geq 3 $ is a prime number and $ \alpha \geq 1 $ is an integer. In these cases, the multiplicative group of reduced residue classes modulo $ m $ is simply the cyclic group of order $ \phi (m) $. In the other cases, the groups of reduced residue classes have a much more complex structure.
Many problems in number theory reduce to the question of the solvability or unsolvability of some type of congruence. As a result of this, the theory of congruences, which was first systematically developed by C.F. Gauss (see [5]) and used by him as a foundation of classical number theory, is to this day one of the basic means of solving number-theoretical problems. In this connection, research into the question of the number of solutions of a congruence equation is of fundamental importance to number theory. The simplest types of congruence equations are congruences of the first degree with one unknown $ ax \equiv b $( $ \mathop{\rm mod}\nolimits \ m $). A complete answer to the question of the number of solutions of congruences of the first degree is provided by the following theorem. Let $ (a,\ m) = d $. The congruence $ ax \equiv b $( $ \mathop{\rm mod}\nolimits \ m $) is unsolvable if $ b $ is not divisible by $ d $. When $ b $ is a multiple of $ d $, the congruence has precisely $ d $ solutions.
The question of the solvability of a system of linear congruences
$$ \sum _ { j=1 } ^ s a _{ij} x _{j} \ \equiv \ b _{i} \ ( \mathop{\rm mod}\nolimits \ p),\ \ i = 1 \dots t, $$
modulo a prime number $ p > 2 $ is solved completely in the general theory of linear equations over arbitrary fields. The case of a composite modulus can be reduced to the case of a prime modulus.
The form of algebraic congruences with one unknown which is the next most complex to study is a two-term congruence
$$ x^{n} \ \equiv \ a \ ( \mathop{\rm mod}\nolimits \ m) \ \ \textrm{ when } \ (a,\ m) = 1. $$
If the congruence $ x^{n} \equiv a \ ( \mathop{\rm mod}\nolimits \ m) $ has solutions, then $ a $ is called an $ n $- th power residue modulo $ m $; if it does not, then $ a $ is called an $ n $- th power non-residue modulo $ m $. More specifically, when $ n=2 $, the residues or non-residues are called quadratic, when $ n=3 $, cubic, and when $ n=4 $, bi-quadratic.
The question of the number of solutions of a congruence
$$ f(x) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ m) $$
modulo a composite number $ m = p _{1} ^ {\alpha _ 1} \dots p _{s} ^ {\alpha _ s} $ reduces to the question of the number of solutions of the congruence
$$ f(x) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ p _{i} ^ {\alpha _ i} ) $$
for every $ i = 1 \dots s $. The following theorem holds: If $ m _{1} \dots m _{r} $ are pairwise relatively prime (coprime) positive integers, then the number $ N $ of solutions of the congruence $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ m _{1} \dots m _{r} $) can be expressed by the values $ N _{i} $, $ i = 1 \dots r $, which are equal to the number of solutions of the corresponding congruences $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ m _{i} $) according to the formula $ N = \prod _ i=1^{r} N _{i} $. In its turn, the question of the number of solutions of the congruence
$$ f(x) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ p^ \alpha ),\ \ \alpha > 1 , $$
generally reduces to the question of the number of solutions of the congruence $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $) where $ p $ is a prime number. The following theorem forms the basis of this reduction: Every solution $ x \equiv x _{1} $( $ \mathop{\rm mod}\nolimits \ p $) of a congruence $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $) can be uniquely continued to a solution $ x \equiv x _ \alpha $( $ \mathop{\rm mod}\nolimits \ p^ \alpha $) of the congruence $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p^ \alpha $) provided that the formal derivative $ f ^ {\ \prime} (x _{1} ) \not\equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $), i.e. a unique solution $ x _ \alpha $ of the congruence $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p^ \alpha $) then exists such that $ x _ \alpha \equiv x _{1} $( $ \mathop{\rm mod}\nolimits \ p $).
A similar situation also arises in the case of a congruence equation in several variables, i.e. in non-degenerate cases the question of the number of solutions of the congruence $ F(x _{1} \dots x _{n} ) = 0 $( $ \mathop{\rm mod}\nolimits \ m $), modulo a composite number $ m $ reduces to the question of the number of solutions of the same congruence modulo a prime number $ m $.
An upper bound for the number of solutions of a congruence $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $), where $ f(x) = a _{0} x^{n} + \dots + a _{n} $, $ a _{0} \not\equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $), is given by Lagrange's theorem: The number of solutions of a congruence $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $) does not exceed the degree of the polynomial $ f(x) $. The study of the question of the exact number of solutions of the congruence $ f(x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $) generally meets with considerable difficulties, so that only a few results have so far (1984) been obtained in this area.
The Lagrange theorem ceases to hold in the case of a composite modulus. The above-mentioned specific property of prime numbers is explained by the fact that the residue classes modulo a prime number $ p $ form a field (see Congruence modulo a prime number). Another specific property of prime numbers which is explained by this fact is expressed in the Wilson theorem.
In the study of quadratic congruences
$$ x^{2} \ \equiv \ a \ ( \mathop{\rm mod}\nolimits \ p) $$
modulo a prime number $ p $, as well as in their applications, the Legendre symbol and the Jacobi symbol are introduced.
Congruence equations modulo a prime number in two unknowns (and generally in any number of unknowns),
$$ F(x,\ y) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ p) , $$
can be treated as equations over the finite prime field of $ p $ elements. Methods of the theory of algebraic functions and algebraic geometry are therefore used in studying them, as well as methods of number theory. Using these methods, an asymptotic expansion in the form
$$ N _{p} \ = \ p + O( \sqrt p ) $$
was first obtained for the number $ N _{p} $ of solutions of a broad class of congruences $ F(x,\ y) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $). The same asymptotic expansions were subsequently deduced using methods of number theory without going beyond the limits of the theory of congruences (see [6]).
Comparatively little is known about algebraic congruences in several unknowns. The following can be considered as a general result (Chevalley's theorem). Let $ F(x _{1} \dots x _{n} ) $ be a polynomial with integer rational coefficients, the degree of which is less than $ n $. The number of solutions of the congruence
$$ F(x _{1} \dots x _{n} ) \ \equiv \ 0 \ ( \mathop{\rm mod}\nolimits \ p) $$
is then divisible by the prime number $ p $. One very strong result for this type of questions was obtained by P. Deligne [9] (see also [10]).
Great value is also attached to research into the question of the number of solutions of congruences in an incomplete residue system. A systematic solution to this type of problems was first attempted by I.M. Vinogradov (see [4]). An example of this type of problems is the problem of the distribution of quadratic residues and non-residues in the set $ 1 \dots p-1 $, which is connected with the study of solutions of the congruence $ y^{2} \equiv x $( $ \mathop{\rm mod}\nolimits \ p $) (see Vinogradov hypotheses; Distribution of power residues and non-residues).
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) MR0195803 Zbl 0145.04902 |
| [2] | B.A. Venkov, "Elementary number theory" , Wolters-Noordhoff (1970) (Translated from Russian) MR0265267 Zbl 0204.37101 |
| [3] | I.M. Vinogradov, "Fundamentals of number theory" , Moscow (1972) (In Russian) |
| [4] | I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) MR0807530 Zbl 0577.01049 |
| [5] | C.F. Gauss, "Untersuchungen über höhere Arithmetik" , Springer (1889) (Translated from Latin) MR0188045 Zbl 21.0166.04 |
| [6] | S.A. Stepanov, "A constructive method in the theory of equations over finite fields" Trudy Mat. Inst. Steklov. , 132 (1973) pp. 237–246 (In Russian) |
| [7] | H. Hasse, "Zahlentheorie" , Akademie Verlag (1963) MR0153659 Zbl 1038.11500 |
| [8] | K. Chandrasekharan, "Introduction to analytic number theory" , Springer (1968) MR0249348 Zbl 0169.37502 |
| [9] | P. Deligne, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–307 MR0340258 Zbl 0314.14007 Zbl 0287.14001 |
| [10] | N.M. Katz, "An overview of Deligne's proof of the Riemann hypothesis for varieties over finite fields" F.E. Browder (ed.) , Mathematical developments arising from Hilbert problems , Proc. Symp. Pure Math. , 28 , Amer. Math. Soc. (1976) pp. 275–305 |
Comments
The simultaneous system of congruences $ x \equiv c _{i} $( $ \mathop{\rm mod}\nolimits \ m _{i} $), $ i = 1 \dots r $, where $ ( m _{i} ,\ m _{j} ) = 1 $ for all $ i \neq j $, has a unique residue class modulo $ M = m _{1} \dots m _{r} $ as solution. This is the content of the Chinese remainder theorem.
The procedure to extend solutions of $ f (x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p $) to solutions of $ f (x) \equiv 0 $( $ \mathop{\rm mod}\nolimits \ p^ \alpha $) is described in the Hensel lemma (cf. [a2]), and extends to a technique in the theory of $ p $- adic numbers (cf. $ p $- adic number).
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. 5; 7; 8 MR0568909 Zbl 0423.10001 |
| [a2] | N. Koblitz, "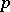 -adic numbers, -adic numbers,  -adic analysis and zeta-functions" , Springer (1977) pp. Chapt. 1 MR466081 -adic analysis and zeta-functions" , Springer (1977) pp. Chapt. 1 MR466081 |
Congruence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Congruence&oldid=23795