Conformal radius of a domain
A characteristic of a conformal mapping of a simply-connected domain, defined as follows: Let 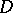 be a simply-connected domain with more than one boundary point in the
be a simply-connected domain with more than one boundary point in the  -plane. Let
-plane. Let 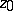 be a point of
be a point of 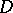 . If
. If 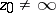 , then there exists a unique function
, then there exists a unique function 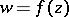 , holomorphic in
, holomorphic in 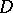 , normalized by the conditions
, normalized by the conditions 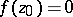 ,
, 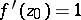 , that maps
, that maps 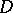 univalently onto the disc
univalently onto the disc 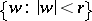 . The radius
. The radius 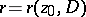 of this disc is called the conformal radius of
of this disc is called the conformal radius of 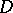 relative to
relative to 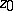 . If
. If 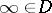 , then there exists a unique function
, then there exists a unique function 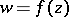 , holomorphic in
, holomorphic in 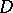 except at
except at 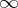 , that, in a neighbourhood of
, that, in a neighbourhood of 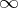 , has a Laurent expansion of the form
, has a Laurent expansion of the form
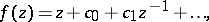 |
and that maps 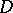 univalently onto a domain
univalently onto a domain 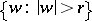 . In this case the quantity
. In this case the quantity 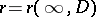 is called the conformal radius of
is called the conformal radius of 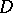 relative to infinity. The conformal radius of
relative to infinity. The conformal radius of 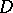 ,
, 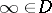 , relative to infinity is equal to the transfinite diameter of the boundary
, relative to infinity is equal to the transfinite diameter of the boundary  of
of 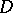 and to the capacity of the set
and to the capacity of the set 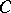 .
.
An extension of the notion of the conformal radius of a domain to the case of an arbitrary domain 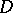 in the complex
in the complex  -plane is that of the interior radius of
-plane is that of the interior radius of 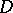 relative to a point
relative to a point 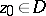 (in the non-Soviet literature the term "interior radius" is used primarily in the case of a simply-connected domain). Let
(in the non-Soviet literature the term "interior radius" is used primarily in the case of a simply-connected domain). Let 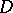 be a domain in the complex
be a domain in the complex  -plane, let
-plane, let 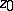 be a point of
be a point of 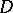 and suppose that a Green function
and suppose that a Green function 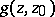 for
for 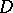 with pole at
with pole at 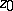 exists. Let
exists. Let 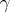 be the Robin constant of
be the Robin constant of 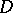 with respect to
with respect to 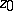 , i.e.
, i.e.
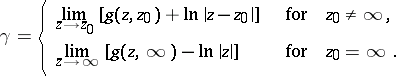 |
The quantity 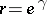 is called the interior radius of
is called the interior radius of 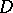 relative to
relative to 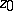 . If
. If 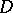 is a simply-connected domain whose boundary contains at least two points, then the interior radius of
is a simply-connected domain whose boundary contains at least two points, then the interior radius of 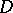 relative to
relative to 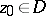 is equal to the conformal radius of
is equal to the conformal radius of 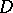 relative to
relative to 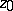 . The interior radius of a domain is non-decreasing as the domain increases: If the domains
. The interior radius of a domain is non-decreasing as the domain increases: If the domains 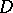 ,
, 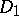 have Green functions
have Green functions 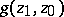 ,
, 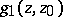 , respectively, if
, respectively, if 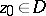 and if
and if 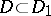 , then the following inequality holds for their interior radii
, then the following inequality holds for their interior radii  ,
, 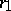 at
at 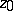 :
:
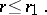 |
The interior radius of an arbitrary domain 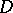 relative to a point
relative to a point 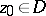 is defined as the least upper bound of the set of interior radii at
is defined as the least upper bound of the set of interior radii at 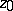 of all domains containing
of all domains containing 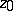 , contained in
, contained in 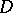 and having a Green function. In accordance with this definition, if
and having a Green function. In accordance with this definition, if 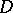 does not have a generalized Green function, then the interior radius
does not have a generalized Green function, then the interior radius  of
of 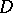 at
at 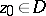 is equal to
is equal to 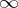 .
.
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | V.I. Smirnov, A.N. Lebedev, "Functions of a complex variable" , M.I.T. (1968) (Translated from Russian) |
| [3] | W.K. Hayman, "Multivalent functions" , Cambridge Univ. Press (1958) |
Comments
In [a2] the conformal radius of a compact connected set  in the
in the  -plane is defined as the conformal radius of its complement relative to infinity (as defined above). If
-plane is defined as the conformal radius of its complement relative to infinity (as defined above). If 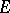 is contained in a disc of radius
is contained in a disc of radius  and has diameter
and has diameter 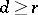 , then
, then
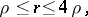 |
where 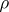 is its conformal radius (in the sense of [a2], cf. [a2]).
is its conformal radius (in the sense of [a2], cf. [a2]).
References
| [a1] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
| [a2] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
Conformal radius of a domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conformal_radius_of_a_domain&oldid=18740