Composition series
composition series
A finite subset 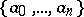 of a partially ordered set with least element
of a partially ordered set with least element  and greatest element
and greatest element  such that
such that
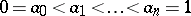 |
and all the intervals  are simple (elementary) (cf. Elementary interval). One can also speak of a composition series of an arbitrary interval
are simple (elementary) (cf. Elementary interval). One can also speak of a composition series of an arbitrary interval  of a partially ordered set. Composition series certainly do not always exists.
of a partially ordered set. Composition series certainly do not always exists.
A composition series of a universal algebra is defined in terms of congruences. Since congruences in groups are defined by normal subgroups, a composition series of a group can be defined as a normal series of it (see Subgroup series) having no proper refinements (without repetition). A series
 |
is a composition series for the group  if and only if every
if and only if every  is a maximal normal subgroup in
is a maximal normal subgroup in 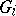 .
.
All the factors  of a composition series are simple groups. Every normal series isomorphic to a composition series is a composition series itself. The Jordan–Hölder theorem holds for composition series of groups. Composition series of rings, and more generally of
of a composition series are simple groups. Every normal series isomorphic to a composition series is a composition series itself. The Jordan–Hölder theorem holds for composition series of groups. Composition series of rings, and more generally of  -groups, are defined in a similar way and have similar properties (see [2]).
-groups, are defined in a similar way and have similar properties (see [2]).
References
| [1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [2] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
Comments
For a universal algebra the notion of a composition series is more precisely defined as follows [1]. Let 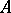 be an
be an  -algebra and
-algebra and 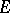 a subalgebra. A normal chain from
a subalgebra. A normal chain from 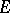 to
to 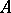 is then a finite chain of subalgebras of
is then a finite chain of subalgebras of 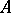 ,
,
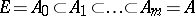 |
together with a congruence 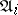 on
on 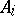 for
for 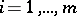 such that
such that  is precisely a
is precisely a 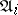 -class. There is a natural notion of refinement and isomorphism of normal chains: normal chains from
-class. There is a natural notion of refinement and isomorphism of normal chains: normal chains from 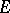 to
to  are isomorphic if and only if they are equally long and if there is a permutation of
are isomorphic if and only if they are equally long and if there is a permutation of 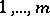 such that
such that  . Then one has the Schreier refinement theorem to the effect that if
. Then one has the Schreier refinement theorem to the effect that if 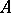 is an
is an  -algebra with subalgebra
-algebra with subalgebra 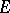 such that on any subalgebra of
such that on any subalgebra of  all congruences commute, then any two normal chains from
all congruences commute, then any two normal chains from 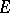 to
to 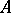 have isomorphic refinements, and the Jordan–Hölder theorem that any two composition series from
have isomorphic refinements, and the Jordan–Hölder theorem that any two composition series from  to
to 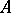 on such an algebra are isomorphic.
on such an algebra are isomorphic.
A subgroup 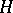 of a group
of a group 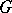 is called subnormal if there is a chain of subgroups
is called subnormal if there is a chain of subgroups  such that
such that 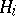 is normal in
is normal in 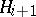 ,
, 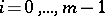 . Consider the lattice of subnormal subgroups
. Consider the lattice of subnormal subgroups 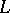 of
of 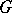 . Then a composition series for the partially ordered set
. Then a composition series for the partially ordered set 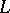 defines in fact a composition series for
defines in fact a composition series for 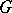 , and vice versa. Something analogous can be formulated for universal algebras (These statements of course do not hold for, respectively, the lattice of normal subgroups and the lattice of congruences.)
, and vice versa. Something analogous can be formulated for universal algebras (These statements of course do not hold for, respectively, the lattice of normal subgroups and the lattice of congruences.)
References
| [a1] | B. Huppert, "Endliche Gruppen" , 1 , Springer (1967) |
Composition series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Composition_series&oldid=13738