Complex torus
A complex Abelian Lie group obtained from the  -dimensional complex space
-dimensional complex space  by factorizing with respect to a lattice
by factorizing with respect to a lattice 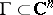 of rank
of rank 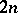 . Every connected compact complex Lie group is a complex torus [1]. Every Hermitian scalar product in
. Every connected compact complex Lie group is a complex torus [1]. Every Hermitian scalar product in 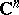 defines on
defines on 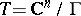 a translation-invariant Kähler metric. Complex tori can also be characterized as the only compact parallelizable Kähler manifolds [2]. The group of automorphisms of the complex manifold
a translation-invariant Kähler metric. Complex tori can also be characterized as the only compact parallelizable Kähler manifolds [2]. The group of automorphisms of the complex manifold 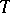 is the same as the holomorph of the group
is the same as the holomorph of the group 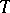 as a complex Lie group (cf. Holomorph of a group).
as a complex Lie group (cf. Holomorph of a group).
Holomorphic 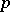 -forms on a complex torus
-forms on a complex torus  have the form
have the form
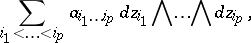 |
where  ,
,  are the coordinates in
are the coordinates in 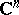 and the Dolbeault cohomology ring
and the Dolbeault cohomology ring 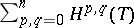 is naturally isomorphic to
is naturally isomorphic to 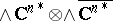 (see [1]).
(see [1]).
As real Lie groups, all  -dimensional complex tori are
-dimensional complex tori are 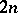 -dimensional tori and are isomorphic for fixed
-dimensional tori and are isomorphic for fixed  . From the point of view of their complex structure their behaviour is extremely complicated. A basis for a lattice
. From the point of view of their complex structure their behaviour is extremely complicated. A basis for a lattice 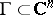 can be given by a matrix
can be given by a matrix  of dimension
of dimension 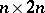 , called the period matrix of the torus
, called the period matrix of the torus 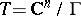 . Tori
. Tori 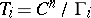 with period matrices
with period matrices 
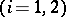 are isomorphic (as complex Lie groups or as complex manifolds) if and only if there exist matrices
are isomorphic (as complex Lie groups or as complex manifolds) if and only if there exist matrices  and
and  such that
such that 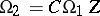 .
.
The period matrix of an  -dimensional torus can be reduced to the form
-dimensional torus can be reduced to the form 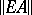 , where
, where 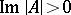 . Tori with matrices of this form generate a holomorphic family that gives an effectively-parametrized versal deformation of any
. Tori with matrices of this form generate a holomorphic family that gives an effectively-parametrized versal deformation of any  -dimensional complex torus depending on
-dimensional complex torus depending on 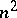 parameters . In particular, for
parameters . In particular, for 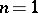 , the parameter space is the upper half-plane
, the parameter space is the upper half-plane 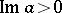 , and the set of isomorphism classes of one-dimensional complex tori can be identified with the quotient
, and the set of isomorphism classes of one-dimensional complex tori can be identified with the quotient  where
where 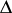 is the modular group.
is the modular group.
Complex tori that are algebraic varieties are called Abelian varieties (cf. Abelian variety). A complex torus  is an Abelian variety if and only there exists in
is an Abelian variety if and only there exists in 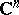 a Hermitian scalar product whose imaginary part is integer-valued on
a Hermitian scalar product whose imaginary part is integer-valued on  [1]. In terms of the period matrix this is the Riemann–Frobenius condition: There should exist a skew-symmetric matrix
[1]. In terms of the period matrix this is the Riemann–Frobenius condition: There should exist a skew-symmetric matrix 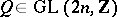 such that
such that  and
and 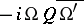 is positive definite. When
is positive definite. When 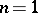 this condition always holds; the corresponding algebraic curves are elliptic (cf. Elliptic curve). The period matrix
this condition always holds; the corresponding algebraic curves are elliptic (cf. Elliptic curve). The period matrix
 |
provides an example of a two-dimensional complex torus that is not an algebraic variety. On this torus there are not even non-constant meromorphic functions [5]. A necessary and sufficient condition that an  -dimensional complex torus be algebraic is the existence on it of
-dimensional complex torus be algebraic is the existence on it of  algebraically-independent meromorphic functions.
algebraically-independent meromorphic functions.
Interest in complex tori originated in the 19th century in connection with the study of Abelian functions (cf. Abelian function) and Jacobi varieties of algebraic curves (cf. Jacobi variety). To any  -dimensional compact Kähler manifold
-dimensional compact Kähler manifold 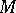 there is related a collection of
there is related a collection of  complex tori, its intermediate Jacobi varieties [7].
complex tori, its intermediate Jacobi varieties [7].
References
| [1] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) |
| [2] | H.C. Wang, "Complex parallisable manifolds" Proc. Amer. Math. Soc. , 5 (1954) pp. 771–776 |
| [3a] | K. Kodaira, D.C. Spencer, "On deformations of complex analytic structures I" Ann. of Math. , 67 (1958) pp. 328–400 |
| [3b] | K. Kodaira, D.C. Spencer, "On deformations of complex analytic structures II" Ann. of Math. , 67 (1958) pp. 403–466 |
| [4] | A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958) |
| [5] | C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955) |
| [6] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
| [7] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) |
Complex torus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complex_torus&oldid=12640