Complex moment problem, truncated
One of the interpolation problems in the complex domain.
Given a doubly indexed finite sequence of complex numbers 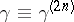 :
:
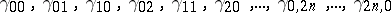 |
with 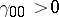 and
and 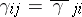 , the truncated complex moment problem entails finding a positive Borel measure
, the truncated complex moment problem entails finding a positive Borel measure 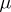 supported in the complex plane
supported in the complex plane 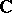 such that
such that
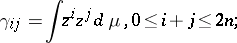 |
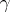 is a truncated moment sequence (of order
is a truncated moment sequence (of order 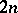 ) and
) and 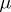 is a representing measure for
is a representing measure for 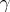 . The truncated complex moment problem serves as a prototype for several other moment problems to which it is closely related: the full complex moment problem prescribes moments of all orders, i.e.,
. The truncated complex moment problem serves as a prototype for several other moment problems to which it is closely related: the full complex moment problem prescribes moments of all orders, i.e., 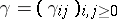 ; the
; the 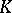 -moment problem (truncated or full) prescribes a closed set
-moment problem (truncated or full) prescribes a closed set 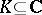 which is to contain the support of the representing measure [a26]; and the multi-dimensional moment problem extends each of these problems to measures supported in
which is to contain the support of the representing measure [a26]; and the multi-dimensional moment problem extends each of these problems to measures supported in 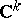 [a14]; moreover, the
[a14]; moreover, the 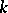 -dimensional complex moment problem is equivalent to the
-dimensional complex moment problem is equivalent to the 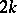 -dimensional real moment problem [a8]. All of these problems generalize classical power moment problems on the real line, whose study was initiated by Th.J. Stieltjes (1894), H. Hamburger (1920–1921), F. Hausdorff (1923), and M. Riesz (1923) (cf. also Moment problem and [a1], [a27]).
-dimensional real moment problem [a8]. All of these problems generalize classical power moment problems on the real line, whose study was initiated by Th.J. Stieltjes (1894), H. Hamburger (1920–1921), F. Hausdorff (1923), and M. Riesz (1923) (cf. also Moment problem and [a1], [a27]).
The truncated complex moment problem is also related to subnormal operator theory [a24], [a29], [a31], polynomial hyponormality [a11], and joint hyponormality [a32], [a33] (cf. also Semi-normal operator). Indeed, A. Atzmon [a2] used subnormal operator theory to solve the full complex moment problem for the disc, and M. Putinar [a18] found a related but different solution to the disc problem based on hyponormal operator theory. More generally, K. Schmüdgen [a26] used an approach based on operator theory and semi-algebraic geometry to obtain the following existence theorem for representing measures [a26] in the multi-dimensional full  -moment problem for the case when
-moment problem for the case when  is compact and semi-algebraic; this result encompasses several previously known special cases (cf. [a4], [a5], [a15], [a17]).
is compact and semi-algebraic; this result encompasses several previously known special cases (cf. [a4], [a5], [a15], [a17]).
Let 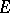 denote the multi-shift operator on multi-sequences and let
denote the multi-shift operator on multi-sequences and let 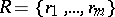 be a finite subset of
be a finite subset of 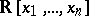 . Suppose that the semi-algebraic set
. Suppose that the semi-algebraic set 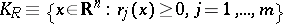 is compact. Then an
is compact. Then an  -dimensional full (real) moment sequence
-dimensional full (real) moment sequence 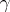 has a representing measure supported in
has a representing measure supported in 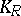 if and only if the quadratic forms associated with
if and only if the quadratic forms associated with 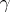 and
and 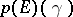 are positive semi-definite (for every
are positive semi-definite (for every 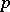 that is a product of distinct
that is a product of distinct 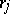 ).
).
For general closed sets 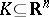 , the full
, the full 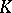 -moment problem continues (1998) to defy a complete solution. Hamburger's classical theorem (1920) gives necessary and sufficient conditions for the solvability of the full moment problem on the real line, i.e.,
-moment problem continues (1998) to defy a complete solution. Hamburger's classical theorem (1920) gives necessary and sufficient conditions for the solvability of the full moment problem on the real line, i.e., 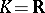 : A real sequence
: A real sequence 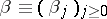 with
with  has a representing measure supported in
has a representing measure supported in 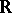 if and only if for each
if and only if for each 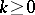 , the Hankel matrix
, the Hankel matrix 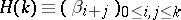 is positive semi-definite (cf. also Nehari extension problem; Synthesis problems). Hamburger's theorem serves as a prototype for much of moment theory, because it provides a concrete criterion closely related to the moments. Nevertheless, when
is positive semi-definite (cf. also Nehari extension problem; Synthesis problems). Hamburger's theorem serves as a prototype for much of moment theory, because it provides a concrete criterion closely related to the moments. Nevertheless, when 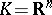 (
(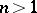 ), positivity alone is not sufficient to imply the existence of a representing measure [a3], [a14], [a25] and a concrete condition for solvability of the
), positivity alone is not sufficient to imply the existence of a representing measure [a3], [a14], [a25] and a concrete condition for solvability of the 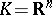 full moment problem (including solvability of the full complex moment problem for
full moment problem (including solvability of the full complex moment problem for 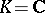 ) remains unknown (to date, 1999, perhaps the most definitive and comprehensive treatments of the full multi-dimensional
) remains unknown (to date, 1999, perhaps the most definitive and comprehensive treatments of the full multi-dimensional 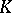 -moment problem can be found in [a38], [a39]).
-moment problem can be found in [a38], [a39]).
In a different direction, M. Riesz (1923) proved that 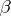 (as above) has a representing measure supported in a closed set
(as above) has a representing measure supported in a closed set 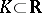 if and only if whenever a polynomial
if and only if whenever a polynomial 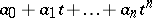 (with complex coefficients) is non-negative on
(with complex coefficients) is non-negative on 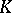 , then
, then 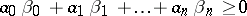 . E.K. Haviland (1935, [a16]) subsequently extended this result to the multi-variable full
. E.K. Haviland (1935, [a16]) subsequently extended this result to the multi-variable full 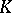 -moment problem. Although Riesz' theorem solves the full moment problem in principle, it is very difficult to verify the Riesz criterion for a particular sequence
-moment problem. Although Riesz' theorem solves the full moment problem in principle, it is very difficult to verify the Riesz criterion for a particular sequence 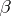 unless
unless 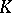 is a half-line (the case studied by Stieltjes), an interval (the case studied by Hausdorff) or, as in Schmüdgen's theorem, when
is a half-line (the case studied by Stieltjes), an interval (the case studied by Hausdorff) or, as in Schmüdgen's theorem, when 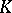 is compact and semi-algebraic. The intractability of the Riesz–Haviland criterion is related to lack of an adequate structure theory for multi-variable polynomials that are non-negative on a given set
is compact and semi-algebraic. The intractability of the Riesz–Haviland criterion is related to lack of an adequate structure theory for multi-variable polynomials that are non-negative on a given set 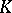 [a5], [a14], [a20], [a22]; in particular, D. Hilbert (1888) established the existence of a polynomial, non-negative on the real plane, that cannot be represented as a sum of squares of polynomials (cf. [a3], [a14], [a25]).
[a5], [a14], [a20], [a22]; in particular, D. Hilbert (1888) established the existence of a polynomial, non-negative on the real plane, that cannot be represented as a sum of squares of polynomials (cf. [a3], [a14], [a25]).
Because a truncated moment problem is finite in nature, one expects that in cases where a truncated moment problem is solvable, it should be possible to explicitly construct finitely atomic representing measures by elementary methods. (See below for such a construction for the truncated complex moment problem.) From this point of view, the multi-variable truncated 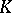 -moment problem subsumes the multi-variable quadrature problem of numerical analysis (cf. [a6], [a13], [a23], [a31]). In addition, J. Stochel [a28] has proven that if
-moment problem subsumes the multi-variable quadrature problem of numerical analysis (cf. [a6], [a13], [a23], [a31]). In addition, J. Stochel [a28] has proven that if 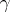 is a multi-variable full moment sequence, and if for each
is a multi-variable full moment sequence, and if for each  the truncated sequence
the truncated sequence 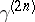 has a representing measure
has a representing measure 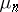 supported in a closed set
supported in a closed set 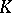 , then some subsequence of
, then some subsequence of 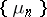 converges (in an appropriate weak topology) to a representing measure
converges (in an appropriate weak topology) to a representing measure 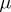 for
for 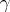 with
with 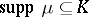 . Thus, a complete solution of the truncated
. Thus, a complete solution of the truncated 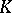 -moment problem would imply a solution to the full
-moment problem would imply a solution to the full 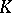 -moment problem.
-moment problem.
Truncated multi-variable moment problems can be analyzed via the positivity and extension properties of the associated moment matrices [a7], [a8]. For the truncated complex moment problem, one associates to 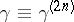 the moment matrix
the moment matrix 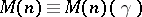 , with rows and columns indexed by
, with rows and columns indexed by 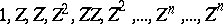 , as follows: the entry in row
, as follows: the entry in row 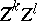 and column
and column 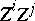 is
is 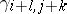 . Thus, if
. Thus, if 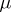 is a representing measure for
is a representing measure for 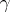 and
and 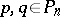 (the set of polynomials in
(the set of polynomials in 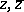 of degree at most
of degree at most  ), then
), then 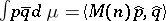 . Here,
. Here, 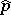 denotes the coefficient vector of
denotes the coefficient vector of 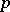 with respect to the above lexicographic ordering of the monomials in
with respect to the above lexicographic ordering of the monomials in 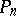 . In particular, it follows that
. In particular, it follows that 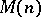 is positive semi-definite and that the support of
is positive semi-definite and that the support of  contains at least
contains at least 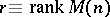 points [a8] (cf. [a30]).
points [a8] (cf. [a30]).
It can be proven [a8] that 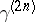 has a rank-
has a rank-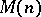 -atomic (minimal) representing measure if and only if
-atomic (minimal) representing measure if and only if 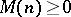 and
and 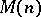 admits an extension to a moment matrix
admits an extension to a moment matrix 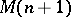 satisfying
satisfying 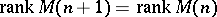 .
.
If 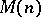 admits such a flat extension
admits such a flat extension 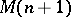 (i.e. an extension that preserves rank), then there is a relation
(i.e. an extension that preserves rank), then there is a relation 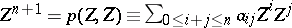 in
in 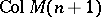 (the column space of
(the column space of 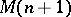 ). It can be shown [a8], Chap. 5, that
). It can be shown [a8], Chap. 5, that  then admits unique successive flat (positive) extensions
then admits unique successive flat (positive) extensions 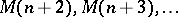 , where
, where 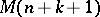 is determined by
is determined by 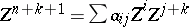 in
in 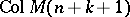 (
(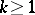 ). The resulting infinite moment matrix
). The resulting infinite moment matrix 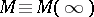 induces a semi-inner product on
induces a semi-inner product on 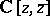 by
by 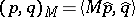 . The space
. The space
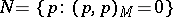 |
is an ideal in 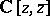 , and
, and 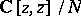 is an
is an  -dimensional Hilbert space on which the multiplication operator
-dimensional Hilbert space on which the multiplication operator 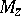 is normal [a8], Chap. 4. The spectrum of
is normal [a8], Chap. 4. The spectrum of 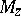 (cf. also Spectrum of a matrix) then provides the support for the unique (
(cf. also Spectrum of a matrix) then provides the support for the unique ( -atomic) representing measure
-atomic) representing measure 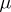 associated with the flat extension
associated with the flat extension 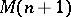 .
.
To explicitly construct 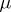 , note that since
, note that since 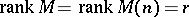 , there is a linear relation
, there is a linear relation 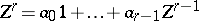 in
in 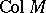 (or, equivalently, in
(or, equivalently, in 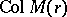 , since
, since 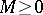 [a12]). The polynomial
[a12]). The polynomial 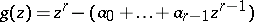 has
has  distinct complex roots,
distinct complex roots, 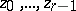 , which provide the support of
, which provide the support of 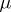 , and the densities
, and the densities 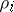 for
for 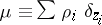 , are uniquely determined by the Vandermonde equation
, are uniquely determined by the Vandermonde equation
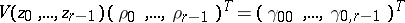 |
[a8], Chap. 4.
Results of [a10] and [a23] imply that the most general finitely atomic representing measures for 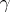 correspond to positive, finite-rank moment matrix extensions
correspond to positive, finite-rank moment matrix extensions 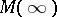 of
of 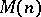 . Such an extension
. Such an extension 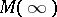 exists if and only if
exists if and only if 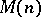 admits a positive extension
admits a positive extension 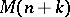 , which in turn admits a flat extension
, which in turn admits a flat extension 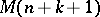 [a10]. Examples for which
[a10]. Examples for which 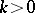 is required are provided in [a37]. On the other hand, examples in [a3], [a25] imply that a positive, infinite rank
is required are provided in [a37]. On the other hand, examples in [a3], [a25] imply that a positive, infinite rank 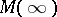 need not correspond to any representing measure for
need not correspond to any representing measure for 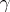 .
.
The preceding results suggest the following flat extension problem [a9], [a10]: under what conditions on 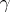 does
does 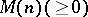 admit a flat extension
admit a flat extension 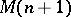 ? Among the necessary conditions for a flat extension is the condition that
? Among the necessary conditions for a flat extension is the condition that 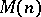 be recursively generated, i.e.
be recursively generated, i.e. 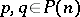 ,
, 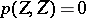 imply
imply 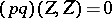 . Although not every recursively generated positive moment matrix admits a flat extension (or even a representing measure [a10], [a36]), several positive results are known:
. Although not every recursively generated positive moment matrix admits a flat extension (or even a representing measure [a10], [a36]), several positive results are known:
i) [a8] If 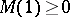 , then
, then 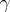 admits a rank-
admits a rank-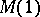 atomic representing measure.
atomic representing measure.
ii) [a9] If 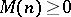 is recursively generated and if there exist
is recursively generated and if there exist 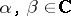 such that
such that 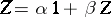 in
in 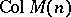 , then
, then 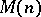 admits infinitely many flat extensions, each corresponding to a distinct rank
admits infinitely many flat extensions, each corresponding to a distinct rank 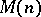 -atomic (minimal) representing measure for
-atomic (minimal) representing measure for 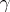 .
.
iii) [a9] If 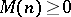 is recursively generated and if
is recursively generated and if 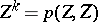 in
in 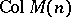 for some
for some 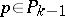 , where
, where 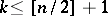 , then
, then 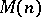 admits a unique flat extension
admits a unique flat extension 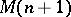 .
.
The preceding approach can be extended to truncated moment problems in any number of real or complex variables; to do this one defines moment matrices subordinate to lexicographic orderings of the variables [a8]. In the case of one real variable, such moment matrices are the familiar Hankel matrices, and the theory subsumes the truncated moment problems of Stieltjes, Hamburger, and Hausdorff [a7] (cf. also Moment problem).
A refinement of the moment matrix technique also leads to an analogue of Schmüdgen's theorem for minimal representing measures in the truncated 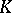 -moment problem for semi-algebraic sets. Given
-moment problem for semi-algebraic sets. Given 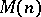 ,
, 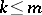 , and a polynomial
, and a polynomial 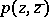 of degree
of degree 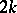 or
or 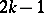 , there exists a unique matrix
, there exists a unique matrix 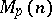 such that
such that 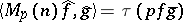 (
(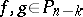 ), where
), where 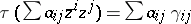 ;
;  may be expressed as a linear combination of compressions of
may be expressed as a linear combination of compressions of 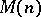 .
.
Let 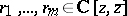 , with
, with 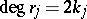 or
or 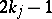 . There exists [a34] a rank-
. There exists [a34] a rank-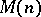 -atomic (minimal) representing measure for
-atomic (minimal) representing measure for 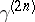 supported in
supported in
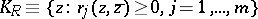 |
if and only if 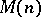 admits a flat extension
admits a flat extension 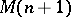 for which
for which 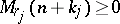 (relative to the uniquely determined flat extension
(relative to the uniquely determined flat extension 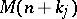 ),
), 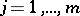 .
.
For additional recent (1999) results on the truncated 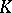 -moment problem, see [a35], [a36].
-moment problem, see [a35], [a36].
References
| [a1] | N.J. Akhiezer, "The classical moment problem" , Hafner (1965) |
| [a2] | A. Atzmon, "A moment problem for positive measures on the unit disc" Pacific J. Math. , 59 (l975) pp. 317–325 |
| [a3] | C. Berg, T.P.R. Christensen, C.U. Jensen, "A remark on the multidimensional moment Problem" Math. Ann. , 223 (1979) pp. 163–169 |
| [a4] | C. Berg, P.H. Maserick, "Polynomially positive definite sequences" Math. Ann. , 259 (1982) pp. 187–495 |
| [a5] | G. Cassier, "Probléme des moments sur un compact de 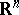 et décomposition des polynômes a plusiers variables" J. Funct. Anal. , 58 (1984) pp. 254–266 et décomposition des polynômes a plusiers variables" J. Funct. Anal. , 58 (1984) pp. 254–266 |
| [a6] | R. Cools, P. Rabinowitz, "Monomial cubature rules since `Stroud': a compilation" J. Comput. Appl. Math. , 48 (1993) pp. 309–326 |
| [a7] | R. Curto, L. Fialkow, "Recursiveness, positivity, and truncated moment problems" Houston J. Math. , 17 (1991) pp. 603–635 |
| [a8] | R. Curto, L. Fialkow, "Solution of the truncated complex moment problem for flat data" Memoirs Amer. Math. Soc. , 119 (1996) |
| [a9] | R. Curto, L. Fialkow, "Flat extensions of positive moment matrices: relations in analytic or conjugate terms" H. Bercovici (ed.) et al. (ed.) , Nonselfadjoint Operator Algebras, Operator Theory, and Related Topics , Birkhäuser (1998) pp. 59–82 |
| [a10] | R. Curto, L. Fialkow, "Flat extensions of positive moment matrices: recursively gnereated relations" Memoirs Amer. Math. Soc. , 136 (1998) |
| [a11] | R. Curto, M. Putinar, "Nearly subnormal operators and moment problems" J. Funct. Anal. , 115 (1993) pp. 480–497 |
| [a12] | L. Fialkow, "Positivity, extensions and the truncated complex moment problem" Contemp. Math. , 185 (1995) pp. 133–150 |
| [a13] | L. Fialkow, "Multivariable quadrature and extensions of moment matrices" Preprint (1996) |
| [a14] | B. Fuglede, "The multidimensional moment problem" Exposition Math. , 1 (1983) pp. 47–65 |
| [a15] | F. Hausdorff, "Momentprobleme fur ein endliches Intervall" Math. Z. , 16 (1923) pp. 220–248 |
| [a16] | E.K. Haviland, "On the momentum problem for distributions in more than one dimension, I–II" Amer. J. Math. , 57/58 (1935/1936) pp. 562–568; 164–168 |
| [a17] | J.L. McGregor, "Solvability criteria for certain 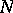 -dimensional moment problems" J. Approx. Th. , 30 (1980) pp. 315–333 -dimensional moment problems" J. Approx. Th. , 30 (1980) pp. 315–333 |
| [a18] | M. Putinar, "A two-dimensional moment problem" J. Funct. Anal. , 80 (1988) pp. 1–8 |
| [a19] | M. Putinar, "The L problem of moments in two dimensions" J. Funct. Anal. , 94 (1990) pp. 288–307 |
| [a20] | M. Putinar, "Positive polynomials on compact semi-algebraic sets" Indiana Univ. Math. J. , 42 (1993) pp. 969–984 |
| [a21] | M. Putinar, "Extremal solutions of the two-dimensional L-problem of moments" J. Funct. Anal. , 136 (1996) pp. 331–364 |
| [a22] | M. Putinar, "Linear analysis of quadrature domains" Ark. Mat. , 33 (1995) pp. 357–376 |
| [a23] | M. Putinar, "On Tchakaloff's theorem" preprint (1995) |
| [a24] | D. Sarason, "Moment problems and operators on Hilbert space" Moments in Math. — Proc. Sympos. Appl. Math. , 37 (1987) pp. 54–70 |
| [a25] | K. Schmüdgen, "An example of a positive polynomial which is not a sum of squares. A positive but not strongly positive functional" Math. Nachr. , 88 (1979) pp. 385–390 |
| [a26] | K. Schmüdgen, "The K-moment problem for semi-a1gebraic sets" Math. Ann. , 289 (1991) pp. 203–206 |
| [a27] | J. Shohat, J. Tamarkin, "The problem of moments" , Math. Surveys , I , Amer. Math. Soc. (1943) |
| [a28] | J. Stochel, "private communication" private communication (1994) |
| [a29] | J. Stochel, F. Szafraniec, "A characterisation of subnormal operators, spectral theory of linear operators and related topics" , Birkhäuser (1984) pp. 261–263 |
| [a30] | J. Stochel, F. Szafraniec, "Algebraic operators and moments on algebraic sets" Portug. Math. , 51 (1994) pp. 1–21 |
| [a31] | V. Tchakaloff, "Formules de cubatures mécaniques à coefficients non négatifs" Bull. Sci. Math. , 81 (1957) pp. 123–134 |
| [a32] | R. Curto, L. Fialkow, "Recursively generated weighted shifts and the subnormal completion problem" Integral Eq. Operator Th. , 17 (1993) pp. 202–216 |
| [a33] | R. Curto, L. Fialkow, "Recursively generated weighted shifts and the subnormal completion problem II" Integral Eq. Operator Th. , 18 (1994) pp. 369–426 |
| [a34] | R. Curto, L. Fialkow, "The truncated complex 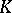 -moment problem" Trans. Amer. Math. Soc. (to appear) -moment problem" Trans. Amer. Math. Soc. (to appear) |
| [a35] | R. Curto, L. Fialkow, "The quadratic moment problem for the unit circle and unit disk" Preprint (1999) |
| [a36] | R. Curto, L. Fialkow, "The quartic complex moment problem" Preprint (1999) |
| [a37] | L. Fialkow, "Minimal representing measures arising from constant rank-increasing moment matrix extensions" J. Operator Th. (to appear) |
| [a38] | M. Putinar, F. Vasilescu, "Solving moment problems by dimensional extension" Preprint (1998) |
| [a39] | J. Stochel, F. Szafraniec, "The complex moment problem and subnormality: A polar decomposition approach" J. Funct. Anal. , 159 (1998) pp. 432–491 |
Complex moment problem, truncated. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complex_moment_problem,_truncated&oldid=15610