Closed system of elements (functions)
A system of elements  of some normed linear space
of some normed linear space 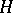 such that any element
such that any element 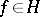 can be approximated with arbitrary accuracy (in the metric of
can be approximated with arbitrary accuracy (in the metric of 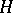 ) by a finite linear combination of elements of the system; in other words: For any
) by a finite linear combination of elements of the system; in other words: For any  there exist numbers
there exist numbers  such that
such that
 | (1) |
For example, the system of powers  ,
, 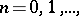 is closed in the space
is closed in the space 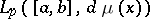 of functions summable in the
of functions summable in the 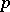 -th degree
-th degree  (or
(or 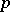 -summable) on a finite interval
-summable) on a finite interval 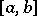 with (integral) weight
with (integral) weight  . The inequality (1) then reads
. The inequality (1) then reads
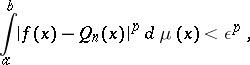 | (2) |
where 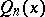 is a polynomial of degree
is a polynomial of degree  . In the most familiar cases,
. In the most familiar cases, 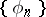 is an orthonormal sequence of elements in a Hilbert space
is an orthonormal sequence of elements in a Hilbert space  . The closure condition (1) is then equivalent to the condition: For all
. The closure condition (1) is then equivalent to the condition: For all 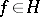 ,
,
 | (3) |
where 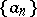 are the Fourier coefficients of
are the Fourier coefficients of 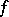 relative to the system
relative to the system 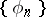 . In the case of a trigonometric system of functions, condition (3) is known as the Parseval identity; explicitly, it takes the form
. In the case of a trigonometric system of functions, condition (3) is known as the Parseval identity; explicitly, it takes the form
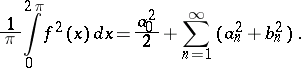 |
This equality was studied by M. Parseval (1806), Ch.J. de la Vallée-Poussin (1890) and A. Hurwitz (1901–1903); a rigorous proof of its validity (for bounded 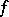 ) was given by A.M. Lyapunov (1896).
) was given by A.M. Lyapunov (1896).
The general case of the closure condition (3) was first examined in detail by V.A. Steklov (1898), in connection with the solution of certain problems in mathematical physics. Introducing the term "closed" , Steklov studied the relevant aspects of various specific systems of orthogonal functions — in particular, the fundamental solutions of the Sturm–Liouville equation (see Sturm–Liouville problem). Equality (3) is therefore often called the Parseval–Steklov closure condition.
The concept of closure is widely applied in the theory of orthogonal polynomials. If the orthogonality interval is finite, a system of orthogonal polynomials is closed for any weight function. For an infinite orthogonality interval, Steklov established various conditions on the weight function that are sufficient to ensure the closure of the corresponding system of orthogonal polynomials; in particular, he proved that the systems of Hermite and Laguerre polynomials are closed. One of Steklov's sufficient conditions for an interval  is the existence of a sequence of positive numbers
is the existence of a sequence of positive numbers 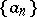 such that
such that
 |
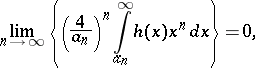 |
where  is a differential weight (function) on
is a differential weight (function) on 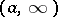 (i.e.
(i.e.  ). A sufficient condition for the entire real line
). A sufficient condition for the entire real line 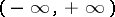 is that
is that 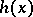 be almost-everywhere positive and satisfy an inequality of the form
be almost-everywhere positive and satisfy an inequality of the form
 |
In a certain sense this condition is "nearly" necessary; indeed, as Steklov proved, a system of polynomials is non-closed if the differential weight function is of the form
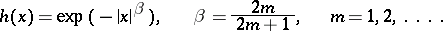 |
A complete solution to the problem of closure conditions for a system of polynomials in 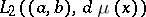 for an infinite interval was given by M. Riesz (1922). He proved that a system of polynomials is closed in
for an infinite interval was given by M. Riesz (1922). He proved that a system of polynomials is closed in  if and only if either the corresponding moment problem is well-defined or, if it is not, that
if and only if either the corresponding moment problem is well-defined or, if it is not, that 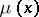 is a so-called
is a so-called  -extremal solution to the moment problem.
-extremal solution to the moment problem.
A concept intimately connected with that of closure is that of completeness of a system of functions: A system of functions is called complete if, whenever a bounded linear functional 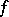 vanishes on all elements of the system
vanishes on all elements of the system 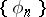 , then
, then 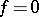 . In a Hilbert space, completeness and closure are equivalent. Completeness of a system
. In a Hilbert space, completeness and closure are equivalent. Completeness of a system 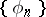 in the space
in the space 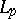 is equivalent to closure of the same system in
is equivalent to closure of the same system in 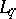 , where
, where 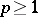 ,
,  and
and 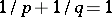 .
.
Analogues of the inequalities (1) or (2) in a complex domain have been studied in detail for systems of polynomials and for more general systems of functions (see Orthogonal polynomials on a complex domain).
References
| [1] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
| [2] | Ya.L. Geronimus, "Theory of orthogonal polynomials. A survey of the achievements in Soviet mathematics" , Moscow-Leningrad (1950) (In Russian) |
| [3] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
| [4a] | V.A. Steklov, Zap. Akad. Nauk Ser. Fiz.-Mat. , 30 : 4 (1911) pp. 1–86 |
| [4b] | V.A. Steklov, Zap. Akad. Nauk Ser. Fiz.-Mat. , 33 : 8 (1914) pp. 1–59 |
| [5] | V.A. Steklov, "Fundamental problems of mathematical physics" , 1–2 , St. Petersburg (1922–1923) (In Russian) |
| [6] | M. Riesz, "Sur le problème des moments et le théorème de Parseval correspondant" Acta Szeged Sect. Math. , 1 (1923) pp. 209–225 Acta Litterarum ac Scientiarum Regiae Universitatis Hungaricae Francisco-Josephine, Sect. Sci. Math. , 1 (1922–1923) pp. 209–225 |
| [7] | E. Hewitt, "Remark on orthonormal sets in 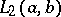 " Amer. Math. Monthly , 61 (1954) pp. 249–250 " Amer. Math. Monthly , 61 (1954) pp. 249–250 |
Comments
References
| [a1] | Ya.L. Geronimus, "Polynomials orthogonal on circle and interval" , Pergamon (1960) (Translated from Russian) |
| [a2] | G. Alexits, "Convergence problems of orthogonal series" , Pergamon (1961) (Translated from German) |
| [a3] | G. Freud, "Orthogonal polynomials" , Pergamon (1971) (Translated from German) |
Closed system of elements (functions). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed_system_of_elements_(functions)&oldid=15299