Chow ring
The ring of rational equivalence classes of algebraic cycles (cf. Algebraic cycle) on a non-singular quasi-projective algebraic variety. Multiplication in this ring is defined in terms of intersections of cycles (cf. Intersection theory).
The Chow ring 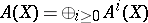 of a variety
of a variety  is a graded commutative ring, where
is a graded commutative ring, where 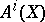 denotes the group of classes of cycles of codimension
denotes the group of classes of cycles of codimension 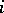 . For a morphism
. For a morphism  the inverse-image homomorphism
the inverse-image homomorphism 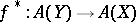 is a homomorphism of rings, and the direct-image homomorphism
is a homomorphism of rings, and the direct-image homomorphism 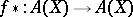 is (for proper
is (for proper 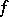 ) a homomorphism of
) a homomorphism of 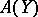 -modules. This means that there is a projection formula:
-modules. This means that there is a projection formula:
 |
The Chow ring is the domain of values for the theory of Chern classes of vector bundles (cf. [1]). More precisely, if  is a locally trivial sheaf of rank
is a locally trivial sheaf of rank  over a variety
over a variety 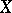 , if
, if  is its projectivization, if
is its projectivization, if 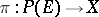 is the canonical projection, and if
is the canonical projection, and if 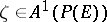 is the class of divisors corresponding to the invertible sheaf
is the class of divisors corresponding to the invertible sheaf 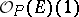 , then
, then 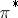 is an imbedding and the Chow ring
is an imbedding and the Chow ring 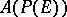 may be identified with the quotient ring of the polynomial ring
may be identified with the quotient ring of the polynomial ring 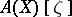 by the ideal generated by the polynomial
by the ideal generated by the polynomial
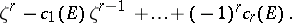 |
The coefficient 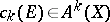 is called the
is called the 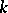 -th Chern class of the sheaf
-th Chern class of the sheaf 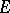 .
.
In the case of a variety over the field of complex numbers, there is a homomorphism 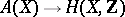 into the singular cohomology ring that preserves the degree and commutes with the inverse-image and direct-image homomorphisms.
into the singular cohomology ring that preserves the degree and commutes with the inverse-image and direct-image homomorphisms.
If 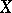 is a singular quasi-projective variety, then its Chow ring
is a singular quasi-projective variety, then its Chow ring 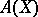 is defined as the direct limit of rings
is defined as the direct limit of rings 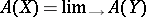 over all morphisms
over all morphisms 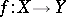 , where
, where 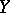 is non-singular. One obtains a contravariant functor into the category of graded rings, satisfying the projection formula (cf. [3]).
is non-singular. One obtains a contravariant functor into the category of graded rings, satisfying the projection formula (cf. [3]).
References
| [1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [2] | "Anneaux de Chow et applications" , Sem. Chevalley (1958) |
| [3] | W. Fulton, "Rational equivalence on singular varieties" Publ. Math. IHES , 45 (1975) pp. 147–167 |
Comments
For 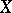 a Noetherian scheme (or ring), let
a Noetherian scheme (or ring), let 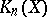 denote the
denote the 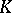 -groups of (the category of) finitely-generated projective modules over
-groups of (the category of) finitely-generated projective modules over 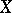 ; cf. Algebraic
; cf. Algebraic 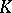 -theory. Let
-theory. Let 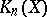 denote the sheaf obtained by sheafifying (in the Zariski topology) the pre-sheaf
denote the sheaf obtained by sheafifying (in the Zariski topology) the pre-sheaf 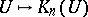 where
where 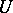 runs through the open (affine) subschemes of
runs through the open (affine) subschemes of 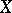 . One then has the Bloch formula [a1]
. One then has the Bloch formula [a1]
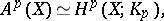 |
providing a link between the Chow groups of 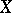 and the cohomology of
and the cohomology of  with values in the
with values in the 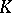 -sheaves of
-sheaves of 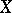 . Using results on the algebraic
. Using results on the algebraic 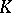 -theory of fields, [a2], this can be used to obtain results on the
-theory of fields, [a2], this can be used to obtain results on the 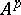 , in particular
, in particular 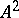 , [a3]. Another often used notation for the Chow group is
, [a3]. Another often used notation for the Chow group is 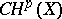 instead of
instead of 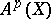 .
.
Cf. Sheaf theory for the notions of sheafification, pre-sheaf, sheaf, and cohomology with values in a sheaf.
References
| [a1] | S. Bloch, "Lectures on algebraic cycles" , Dept. Math. Duke Univ. (1980) |
| [a2] | A.S. Merkur'ev, A.A. Suslin, "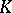 -cohomology of Severi–Brauer varieties and norm residue homomorphism" Math. USSR Izv. , 21 (1983) pp. 307–340 Izv. Akad. Nauk SSSR Ser. Mat. , 46 : 5 (1982) pp. 1011–1046 -cohomology of Severi–Brauer varieties and norm residue homomorphism" Math. USSR Izv. , 21 (1983) pp. 307–340 Izv. Akad. Nauk SSSR Ser. Mat. , 46 : 5 (1982) pp. 1011–1046 |
| [a3] | J.-L. Colliot-Thélène, "Hilbert's theorem 90 for 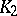 with application to the Chow groups of rational surfaces" Inv. Math. , 71 (1983) pp. 1–20 with application to the Chow groups of rational surfaces" Inv. Math. , 71 (1983) pp. 1–20 |
| [a4] | W. Fulton, "Intersection theory" , Springer (1984) |
Chow ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chow_ring&oldid=16740