Chern character
A characteristic class defining a ring homomorphism  . For a one-dimensional bundle
. For a one-dimensional bundle  there is the identity
there is the identity  , where
, where  is the rational Chern class. This identity, together with the requirement that the class
is the rational Chern class. This identity, together with the requirement that the class  define a homomorphism
define a homomorphism  , uniquely determines the class
, uniquely determines the class 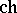 . There is a commutative diagram
. There is a commutative diagram
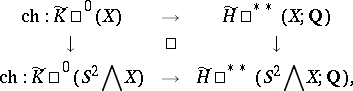 |
in which the vertical arrows denote the periodicity operator and the dual suspension. Let the mapping
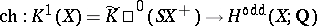 |
coincide with the composition
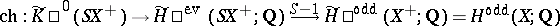 |
(here "+" denotes the functor from the category of topological spaces into the category of pointed spaces  . One obtains a functorial transformation
. One obtains a functorial transformation 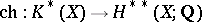 , and this induces a transformation
, and this induces a transformation 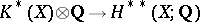 , which is a natural isomorphism of
, which is a natural isomorphism of  -graded rings.
-graded rings.
If  is a generalized cohomology theory in which the Chern classes
is a generalized cohomology theory in which the Chern classes 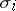 are defined, then for one-dimensional bundles
are defined, then for one-dimensional bundles 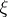 the generalized Chern character
the generalized Chern character
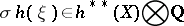 |
is defined by the formula
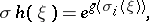 |
where  is the logarithm of the formal group corresponding to the theory
is the logarithm of the formal group corresponding to the theory  . By the splitting lemma one can define a natural ring homomorphism
. By the splitting lemma one can define a natural ring homomorphism
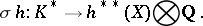 |
For a generalized cohomology theory  there exists a unique natural isomorphism of graded groups
there exists a unique natural isomorphism of graded groups 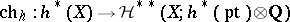 , which for
, which for  coincides with the mapping
coincides with the mapping
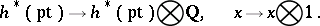 |
Here
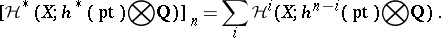 |
The mapping  , where
, where 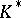 is a
is a 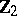 -graded
-graded 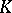 -theory, coincides with the Chern character
-theory, coincides with the Chern character 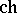 . The natural transformation functor
. The natural transformation functor 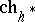 is called the Chern–Dold character.
is called the Chern–Dold character.
Let 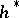 be the unitary cobordism theory
be the unitary cobordism theory 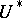 and let
and let  be the space
be the space 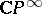 . The ring
. The ring  is isomorphic to the ring of formal power series
is isomorphic to the ring of formal power series  , where
, where  and
and 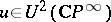 is the orientation of the bundle
is the orientation of the bundle 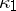 . Analogously, the ring
. Analogously, the ring 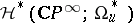 is isomorphic to
is isomorphic to 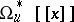 , where
, where 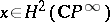 is the orientation of
is the orientation of  . The formal power series
. The formal power series 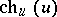 is the functional inverse of the Mishchenko series
is the functional inverse of the Mishchenko series
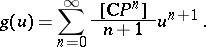 |
For references see Chern class.
Comments
Cf. the comments to Chern class and Chern number.
Chern character. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chern_character&oldid=14027