Chebyshev system
A system of linearly independent functions  in a space
in a space  with the property that no non-trivial polynomial in this system has more than
with the property that no non-trivial polynomial in this system has more than 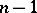 distinct zeros. An example of a Chebyshev system in
distinct zeros. An example of a Chebyshev system in 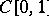 is the system
is the system 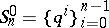 ,
,  ; its approximation properties in the uniform metric were first studied by P.L. Chebyshev [1]. The term "Chebyshev system" was introduced by e theory of functions','../c/c025430.htm','Continuation method (to a parametrized family)','../c/c025520.htm','Euler–Lagrange equation','../e/e036510.htm','Fourier series','../f/f041090.htm','Functions of a real variable, theory of','../f/f042130.htm','Hilbert problems','../h/h120080.htm','Jackson inequality','../j/j054000.htm','Laplace theorem','../l/l057530.htm','Lebesgue constants','../l/l057800.htm','Limit theorems','../l/l058920.htm','Linear elliptic partial differential equation and system','../l/l059180.htm','Lyapunov theorem','../l/l061200.htm','Mathematical statistics','../m/m062710.htm','Minimal surface','../m/m063920.htm','Markov–Bernstein-type inequalities','../m/m110060.htm','Ornstein–Uhlenbeck process','../o/o070240.htm','Orthogonal polynomials','../o/o070340.htm','Plateau problem, multi-dimensional','../p/p072850.htm','Quasi-analytic class','../q/q076370.htm')" style="background-color:yellow;">S.N. Bernshtein [2]. An arbitrary Chebyshev system inherits practically all approximation properties of the system
; its approximation properties in the uniform metric were first studied by P.L. Chebyshev [1]. The term "Chebyshev system" was introduced by e theory of functions','../c/c025430.htm','Continuation method (to a parametrized family)','../c/c025520.htm','Euler–Lagrange equation','../e/e036510.htm','Fourier series','../f/f041090.htm','Functions of a real variable, theory of','../f/f042130.htm','Hilbert problems','../h/h120080.htm','Jackson inequality','../j/j054000.htm','Laplace theorem','../l/l057530.htm','Lebesgue constants','../l/l057800.htm','Limit theorems','../l/l058920.htm','Linear elliptic partial differential equation and system','../l/l059180.htm','Lyapunov theorem','../l/l061200.htm','Mathematical statistics','../m/m062710.htm','Minimal surface','../m/m063920.htm','Markov–Bernstein-type inequalities','../m/m110060.htm','Ornstein–Uhlenbeck process','../o/o070240.htm','Orthogonal polynomials','../o/o070340.htm','Plateau problem, multi-dimensional','../p/p072850.htm','Quasi-analytic class','../q/q076370.htm')" style="background-color:yellow;">S.N. Bernshtein [2]. An arbitrary Chebyshev system inherits practically all approximation properties of the system  .
.
The Chebyshev theorem and the de la Vallée-Poussin theorem (on alternation) remain valid for Chebyshev systems; all methods developed for the approximate construction of algebraic polynomials of best uniform approximation apply equally well and the uniqueness theorem for polynomials of best uniform approximation is valid for Chebyshev systems (see also Haar condition; Chebyshev set). A compact set  admits a Chebyshev system of degree
admits a Chebyshev system of degree 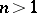 if and only if
if and only if 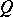 is homeomorphic to the circle or to a subset of it (
is homeomorphic to the circle or to a subset of it (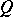 is not homeomorphic to the circle when
is not homeomorphic to the circle when  is even). In particular, there is no Chebyshev system on any
is even). In particular, there is no Chebyshev system on any 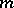 -dimensional domain
-dimensional domain 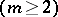 , for example on a square [3].
, for example on a square [3].
As an example of a system that is not a Chebyshev system, one can mention the system consisting of splines (cf. Spline) of degree 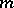 with
with  fixed knots
fixed knots 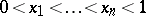 . In this case the function
. In this case the function 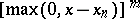 belongs to the system, and has infinitely many zeros. Lack of uniqueness makes the numerical construction of best approximations difficult.
belongs to the system, and has infinitely many zeros. Lack of uniqueness makes the numerical construction of best approximations difficult.
An important special case of a Chebyshev system is a Markov function system.
References
| [1] | P.L. Chebyshev, "Questions on smallest quantities connected with the approximate representation of functions (1859)" , Collected works , 2 , Moscow-Leningrad (1947) pp. 151–238 (In Russian) |
| [2] | S.N. Bernshtein, "Extremal properties of polynomials and best approximation of continuous functions of a real variable" , 1 , Moscow-Leningrad (1937) (In Russian) |
| [3] | J.C. Mairhuber, "On Haar's theorem concerning Chebyshev approximation problems having unique solutions" Proc. Amer. Math. Soc. , 7 : 4 (1956) pp. 609–615 |
| [4] | V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian) |
| [5] | S. Karlin, V. Studden, "Tchebycheff systems with applications in analysis and statistics" , Interscience (1966) |
Comments
References
| [a1] | G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966) pp. Chapt. 2, Sect. 4 |
| [a2] | R. Zielke, "Discontinuous Čebyšev systems" , Springer (1979) |
Chebyshev system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_system&oldid=12169