Chebyshev set
A set  in a metric space
in a metric space  such that for each
such that for each  there exists exactly one element of best approximation, that is, an element
there exists exactly one element of best approximation, that is, an element  such that
such that  . The existence and uniqueness of best approximating elements is a most simple condition, most convenient from the theoretical as well as from the practical point of view. This determines the role of Chebyshev sets in approximation theory and in the theory of Banach spaces. The notion of a Chebyshev set is a logical development of that of a Chebyshev system.
. The existence and uniqueness of best approximating elements is a most simple condition, most convenient from the theoretical as well as from the practical point of view. This determines the role of Chebyshev sets in approximation theory and in the theory of Banach spaces. The notion of a Chebyshev set is a logical development of that of a Chebyshev system.
A finite-dimensional vector subspace  with basis
with basis  is a Chebyshev set (Chebyshev subspace) if and only if the functions
is a Chebyshev set (Chebyshev subspace) if and only if the functions  form a Chebyshev system (equivalently, satisfy the Haar condition). Lines, planes, convex figures, and bodies in a Euclidean space are Chebyshev sets. Non-trivial examples of Chebyshev sets were first considered by P.L. Chebyshev [1]. These were the subspace of algebraic polynomials of degree
form a Chebyshev system (equivalently, satisfy the Haar condition). Lines, planes, convex figures, and bodies in a Euclidean space are Chebyshev sets. Non-trivial examples of Chebyshev sets were first considered by P.L. Chebyshev [1]. These were the subspace of algebraic polynomials of degree  and the set of rational functions with fixed degree of the numerator and the denominator in the space
and the set of rational functions with fixed degree of the numerator and the denominator in the space  . A set in a Euclidean space is a Chebyshev set if and only if it is closed and convex.
. A set in a Euclidean space is a Chebyshev set if and only if it is closed and convex.
In Lobachevskii geometry a Chebyshev set need not be convex [7]. In a two-dimensional non-smooth normed space it is easy to construct a non-convex Chebyshev set. There exist non-smooth three-dimensional spaces in which every Chebyshev set is convex. The problem whether arbitrary Chebyshev sets in a Hilbert space are convex is unsolved (1987). At the same time there are proofs of the convexity of Chebyshev sets under supplementary conditions on the set and on the space, and conditions that are equivalent to convexity for Chebyshev sets (cf. Approximate compactness).
Since Chebyshev sets can be non-convex, one studies other characteristics of them. A Chebyshev set 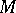 is called a sun [2] if for any
is called a sun [2] if for any  and
and 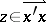 (where
(where 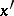 is the point of
is the point of 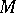 nearest to
nearest to  and
and 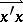 is the ray through
is the ray through  emanating from
emanating from  ), the point
), the point  is the point of
is the point of 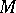 nearest to
nearest to  . For a Chebyshev set
. For a Chebyshev set 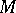 in a smooth space, the conditions "M is convex" and "M is a sun" are equivalent.
in a smooth space, the conditions "M is convex" and "M is a sun" are equivalent.
The properties of Chebyshev sets are closely related to approximative compactness and the continuity of a metric projection. Let 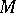 be a given Chebyshev set in a Banach space
be a given Chebyshev set in a Banach space  . If a)
. If a) 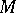 is a boundedly-compact set or b)
is a boundedly-compact set or b) 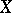 is uniformly convex and
is uniformly convex and 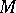 is locally compact, then
is locally compact, then 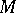 is a sun (under the extra hypothesis "X is smooth" ,
is a sun (under the extra hypothesis "X is smooth" , 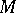 is a convex set). A Chebyshev set with a continuous metric projection in a smooth reflexive space is convex, and in
is a convex set). A Chebyshev set with a continuous metric projection in a smooth reflexive space is convex, and in 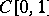 it is a sun. Every Chebyshev set in a uniformly-convex Banach space is connected (even its intersections with balls are connected). However, the set of functions
it is a sun. Every Chebyshev set in a uniformly-convex Banach space is connected (even its intersections with balls are connected). However, the set of functions 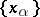 in
in 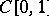 , where
, where  ,
,  and
and 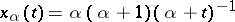 for
for 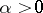 , is a Chebyshev set with an isolated point, that is, it is not connected and it is not a sun [8]. The question whether, in an arbitrary Banach space, every Chebyshev set that is a sun is connected, remains unsolved (1987).
, is a Chebyshev set with an isolated point, that is, it is not connected and it is not a sun [8]. The question whether, in an arbitrary Banach space, every Chebyshev set that is a sun is connected, remains unsolved (1987).
In "nice" spaces there are quite a number of Chebyshev sets. In a Banach space 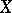 every convex closed set is a Chebyshev set if and only if
every convex closed set is a Chebyshev set if and only if 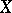 is strictly convex (strictly normed) and reflexive. In an arbitrary reflexive space there always exists a Chebyshev set, to wit a hyperplane. In an
is strictly convex (strictly normed) and reflexive. In an arbitrary reflexive space there always exists a Chebyshev set, to wit a hyperplane. In an  -dimensional Banach space there exist Chebyshev subspaces of all dimensions
-dimensional Banach space there exist Chebyshev subspaces of all dimensions 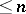 (cf. [9]). There exists a space in which there are no non-trivial Chebyshev subspaces. In a uniformly-convex Banach space
(cf. [9]). There exists a space in which there are no non-trivial Chebyshev subspaces. In a uniformly-convex Banach space 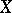 , every closed subset
, every closed subset 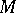 is an almost Chebyshev set, in the sense that the set of points
is an almost Chebyshev set, in the sense that the set of points 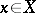 for which a unique nearest point in
for which a unique nearest point in 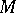 exists, is the complement of a meager set in
exists, is the complement of a meager set in 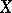 . In a separable space there exist subspaces of all finite dimensions that are "almost Chebyshev sets" . There exists a space, isomorphic to a Hilbert space, in which the metric projection onto a certain Chebyshev subspace is discontinuous.
. In a separable space there exist subspaces of all finite dimensions that are "almost Chebyshev sets" . There exists a space, isomorphic to a Hilbert space, in which the metric projection onto a certain Chebyshev subspace is discontinuous.
The notion of a Chebyshev set allows generalizations, for example, instead of the uniqueness of the element of best approximation one may require some kind of "regularity" of the set of elements of best approximation for each 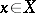 , such as compactness, connectedness or convexity. The results obtained for such generalizations are largely analogous to the corresponding results for Chebyshev sets.
, such as compactness, connectedness or convexity. The results obtained for such generalizations are largely analogous to the corresponding results for Chebyshev sets.
References
| [1] | P.L. Chebyshev, "Questions on smallest quantities connected with the approximate representation of functions (1859)" , Collected works , 2 , Moscow-Leningrad (1947) pp. 151–235 (In Russian) |
| [2] | N.V. Efimov, S.B. Stechkin, "Some properties of Chebyshev sets" Dokl. Akad. Nauk SSSR , 118 : 1 (1958) pp. 17–19 (In Russian) |
| [3] | A.L. Garkavi, "The theory of best approximation in normed linear spaces" Itogi Nauk. Mat. Anal. 1967 (1969) pp. 75–132 (In Russian) |
| [4] | L.P. Vlasov, "Approximative properties of sets in normed linear spaces" Russian Math. Surveys , 28 : 6 (1973) pp. 1–66 Uspekhi Mat. Nauk , 28 : 6 (1973) pp. 3–66 |
| [5] | I.M. Singer, "Best approximation in normed linear spaces by elements of linear subspaces" , Springer (1970) |
| [6] | I.M. Singer, "The theory of best approximation and functional analysis" , CBMS Regional Conf. Ser. , 13 , SIAM (1974) |
| [7] | V.G. Boltyanskii, I.M. Yaglom, "Convex figures and bodies" , Encyclopaedia of elementary mathematics , 5 , Moscow (1966) pp. 181–269 (In Russian) |
| [8] | C.B. Dunham, "Chebyshev sets in 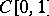 which are not suns" Canad. Math. Bull. , 18 : 1 (1975) pp. 35–37 which are not suns" Canad. Math. Bull. , 18 : 1 (1975) pp. 35–37 |
| [9] | V.A. Zalgaller, "On 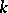 -dimensional directions, special for a convex body -dimensional directions, special for a convex body 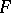 in in 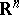 " Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. , 27 (1972) pp. 67–72 (In Russian) " Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. , 27 (1972) pp. 67–72 (In Russian) |
Comments
For the notion of a smooth real linear vector space cf. Smooth space.
References
| [a1] | F. Deutsch, "Existence of best approximations" J. Approx. Theory , 28 (1980) pp. 132–154 |
Chebyshev set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_set&oldid=19276