Character of a representation of an associative algebra

A function 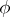on the associative algebra 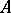defined by the formula 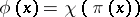for , where 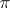is a representation of 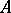and 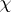is a linear functional defined on some ideal 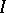in , satisfying the condition 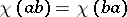for all 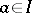, . If the representation 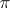is finite-dimensional or if the algebra contains a non-zero finite-dimensional operator, then for 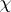one usually considers the trace of the operator. Let 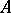be a -algebra, 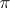a representation of the -algebra 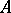such that the von Neumann algebra 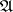generated by is a factor of semi-finite type; let be a faithful normal semi-finite trace on 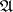and let 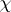be a linear extension of 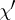to an ideal 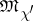. 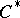If the set is non-zero, then the formula , , determines a character of the representation of the algebra whose restriction to is a character of the -algebra 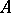(cf. Character of a 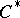-algebra). In many cases the character of a representation of an algebra determines the representation uniquely, up to a certain equivalence relation; for example, the character of an irreducible finite-dimensional representation determines the representation uniquely up to equivalence; the character of a factor representation of a 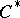-algebra admitting a trace determines the representation uniquely up to quasi-equivalence.

References

[1]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)
[2]	C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)
[3]	J. Dixmier, "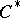 algebras" , North-Holland (1977) (Translated from French)