Character of a representation of a group

In the case of a finite-dimensional representation 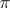this is the function 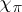on the group 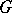defined by the formula

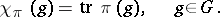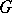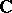For arbitrary continuous representations of a topological group over this definition is generalized as follows:

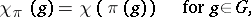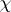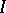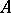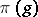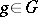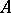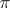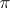where is a linear functional defined on some ideal of the algebra generated by the family of operators , , that is invariant under inner automorphisms of . In certain cases the character of a representation is defined as that of the representation of a certain group algebra of determined by (see Character of a representation of an associative algebra).

The character of a direct sum (of a tensor product) of finite-dimensional representations is equal to the sum (the product) of the characters of these representations. The character of a finite-dimensional representation of a group is a function that is constant on classes of conjugate elements; the character of a continuous finite-dimensional unitary representation of a group is a continuous positive-definite function on the group.

In many cases the character of a representation of a group determines the representation uniquely up to equivalence; for example, the character of an irreducible finite-dimensional representation over a field of characteristic 0 determines the representation uniquely up to spatial equivalence; the character of a finite-dimensional continuous unitary representation of a compact group is determining up to unitary equivalence.

The character of a representation of a locally compact group 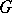admitting an extension to a representation of the algebra of continuous functions of compact support on 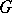can be defined by a measure on 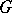; in particular, the character of the regular representation of a unimodular group is given by a probability point measure concentrated at the unit element of . The character of a representation 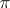of a Lie group 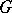admitting an extension to a representation of the algebra 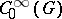of infinitely-differentiable functions of compact support on 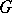can be defined as a generalized function on 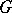. If 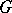is a nilpotent or a linear semi-simple Lie group, then the characters of irreducible unitary representations 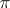of 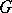are defined by locally integrable functions 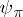according to the formula

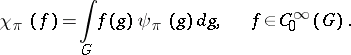These characters determine the representation 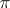uniquely up to unitary equivalence.

If the group 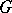is compact, every continuous positive-definite function on 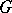that is constant on classes of conjugate elements can be expanded into a series with respect to the characters of the irreducible representations 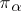of 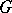. The series converges uniformly on 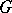and the characters 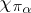form an orthonormal system in the space 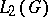that is complete in the subspace of functions in 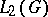that are constant on classes of conjugate elements in 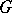. If 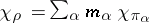is the expansion of the character of a continuous finite-dimensional representation 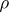of the group 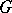with respect to the characters 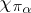, then the 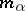are integers, namely, the multiplicities with which the 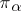occur in 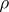. 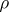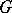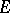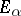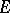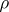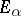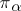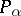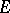If is a continuous representation of in a quasi-complete, barrelled, locally convex topological space , then there exists a maximal subspace of such that the restriction of to is a multiple of , and there is a continuous projection of onto 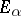, defined by

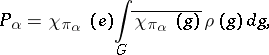where 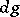is the Haar measure on 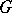for which .

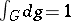References

[1]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)
[2]	C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962)
[3]	J. Dixmier, "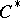 algebras" , North-Holland (1977) (Translated from French)
[4]	G.F. Frobenius, J.-P. Serre (ed.) , Gesammelte Abhandlungen , Springer (1968)
[5]	M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)
[6]	D.E. Littlewood, "The theory of group characters and matrix representations of groups" , Clarendon Press (1950)