Character of a group
A homomorphism of the given group into some standard Abelian group  . Usually,
. Usually,  is taken to be either the multiplicative group
is taken to be either the multiplicative group  of a field
of a field  or the subgroup
or the subgroup
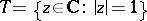 |
of  . The concept of a character of a group was originally introduced for finite groups
. The concept of a character of a group was originally introduced for finite groups  with
with  (in this case every character
(in this case every character  takes values in
takes values in 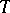 ).
).
The study of characters of groups reduces to the case of Abelian groups, since there is a natural isomorphism between the groups  and
and 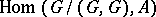 , where
, where  is the commutator subgroup of
is the commutator subgroup of 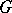 . The characters
. The characters 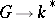 form a linearly independent system in the space of all
form a linearly independent system in the space of all  -valued functions on
-valued functions on 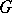 . A character
. A character  extends uniquely to a character of the group algebra
extends uniquely to a character of the group algebra  . The characters
. The characters  are one-dimensional linear representations of
are one-dimensional linear representations of 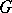 over
over  ; the concept of a character of a representation of a group coincides in the one-dimensional case with the concept of a character of a group. Sometimes characters of a group are understood to mean characters of any of its finite-dimensional representations (and even to mean the representations themselves).
; the concept of a character of a representation of a group coincides in the one-dimensional case with the concept of a character of a group. Sometimes characters of a group are understood to mean characters of any of its finite-dimensional representations (and even to mean the representations themselves).
A character of a topological group 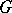 is a continuous homomorphism
is a continuous homomorphism  . If
. If  is a locally compact Abelian group, then its characters separate points, that is, for any
is a locally compact Abelian group, then its characters separate points, that is, for any  ,
,  , there exists a character
, there exists a character 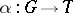 such that
such that  . For Hausdorff Abelian groups
. For Hausdorff Abelian groups  this assertion is not true, in general (see [3]). A character of an algebraic group
this assertion is not true, in general (see [3]). A character of an algebraic group 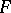 over an algebraically closed field
over an algebraically closed field  is a rational homomorphism
is a rational homomorphism  .
.
In number theory an important role is played by the characters of the multiplicative group  of the residue ring
of the residue ring  modulo
modulo 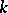 , which correspond one-to-one to Dirichlet characters modulo
, which correspond one-to-one to Dirichlet characters modulo 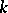 : To a character
: To a character  there corresponds the Dirichlet character
there corresponds the Dirichlet character  given by the formula
given by the formula
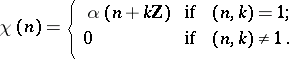 |
See also Character group.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | S.A. Morris, "Pontryagin duality and the structure of locally compact Abelian groups" , London Math. Soc. Lecture Notes , 29 , Cambridge Univ. Press (1977) |
| [3] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1 , Springer (1963) |
Character of a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Character_of_a_group&oldid=16966