Cauchy test
The Cauchy criterion for the convergence of a series: Given a series $\sum_{n=1}^{\infty}u_n$ with non-negative real terms, if there exists a number $q$, $0\leq q<1$, such that, for all sufficiently large $n$, one has the inequality $(u_n)^{1/n}\leq q$, which is equivalent to the condition 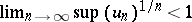 , then the series is convergent. Conversely, if for all sufficiently large
, then the series is convergent. Conversely, if for all sufficiently large  one has the inequality
one has the inequality 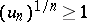 , or even the weaker condition: There exists a subsequence
, or even the weaker condition: There exists a subsequence 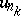 ,
, 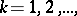 with terms satisfying the inequality
with terms satisfying the inequality 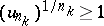 , then the series is divergent.
, then the series is divergent.
In particular, if 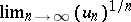 exists and is
exists and is 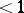 , then the series
, then the series 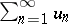 is convergent; if it is
is convergent; if it is 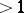 , then the series
, then the series 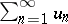 is divergent. This was proved by A.L. Cauchy . In the case of a series
is divergent. This was proved by A.L. Cauchy . In the case of a series 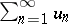 with terms
with terms 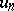 of arbitrary sign, the condition
of arbitrary sign, the condition 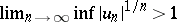 implies that the series is divergent; if
implies that the series is divergent; if 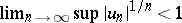 , the series is absolutely convergent.
, the series is absolutely convergent.
The integral Cauchy test, or the Cauchy–MacLaurin integral criterion: Given a series 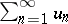 with non-negative real terms, if there exists a non-increasing non-negative function
with non-negative real terms, if there exists a non-increasing non-negative function 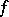 , defined for
, defined for 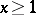 , such that
, such that 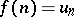 ,
, 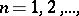 then the series is convergent if and only if the integral
then the series is convergent if and only if the integral 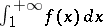 is convergent. This test was first presented in a geometrical form by C. MacLaurin [2], and later rediscovered by A.L. Cauchy [3].
is convergent. This test was first presented in a geometrical form by C. MacLaurin [2], and later rediscovered by A.L. Cauchy [3].
References
| [1] | A.L. Cauchy, "Analyse algébrique" , Gauthier-Villars (1821) pp. 132–135 (German translation: Springer, 1885) |
| [2] | C. MacLaurin, "Treatise of fluxions" , 1 , Edinburgh (1742) pp. 289–290 |
| [3] | A.L. Cauchy, "Sur la convergence des séries" , Oeuvres complètes Ser. 2 , 7 , Gauthier-Villars (1889) pp. 267–279 |
| [4] | S.M. Nikol'skii, "A course of mathematical analysis" , 1 , MIR (1977) (Translated from Russian) |
Comments
See also Cauchy criteria. The following is also known as Cauchy's condensation test or Cauchy's convergence theorem (criterion): If the terms 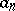 of a series
of a series 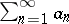 form a monotone decreasing sequence, then
form a monotone decreasing sequence, then 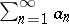 and
and
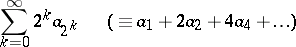 |
are equiconvergent series, i.e. both converge or both diverge (cf. [a1], [a2]).
References
| [a1] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
| [a2] | G.H. Hardy, "A course of pure mathematics" , Cambridge Univ. Press (1975) |
Cauchy test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_test&oldid=29316