Catenary
The plane transcendental curve describing the form of a homogeneous flexible string of fixed length and with fixed ends attained under the action of gravity (see Fig.).
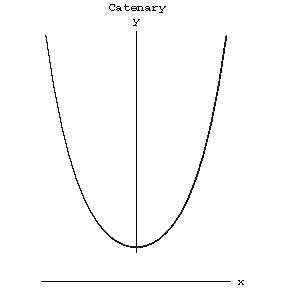
Figure: c020790a
In Cartesian coordinates its equation is $$ y= \frac{a}{2} \left( e^{x/a} + e^{-x/a} \right) = a \cosh \frac{x}{a} $$
The length of an arc beginning at the point $x=0$ is $$ l= \frac{1}{2} \left( e^{x/a} - e^{-x/a} \right) = a \sinh \frac{x}{a} $$
The radius of curvature is $$ r= a \cosh^2 \frac{x}{a} $$
The area bounded by an arc of the catenary, two of its ordinates and the $y$-axis is $$ S = a \sqrt{ y_2^2 - a^2 } - a \sqrt{ y_1^2 - a^2 } = a^2 \left( \sinh \frac{x_2}{a} - \sinh \frac{x_1}{a} \right) $$
If an arc of a catenary is rotated around the $x$-axis, it forms a catenoid.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
Catenary. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Catenary&oldid=38914