Calibre
of a topological space 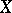
A cardinal number  such that every family
such that every family 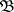 of cardinality
of cardinality  , consisting of non-empty open subsets of a topological space
, consisting of non-empty open subsets of a topological space 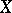 , contains a subset
, contains a subset 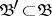 , also of cardinality
, also of cardinality  , with non-empty intersection, i.e.
, with non-empty intersection, i.e. 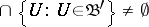 . A regular uncountable cardinal number
. A regular uncountable cardinal number  is a calibre of a topological product
is a calibre of a topological product 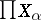 ,
, 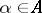 , if and only if
, if and only if  is a calibre of every factor
is a calibre of every factor 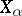 . The property of being a calibre is preserved under continuous mappings; every uncountable regular cardinal number is a calibre of any dyadic compactum. If the first uncountable cardinal number is a calibre of a space
. The property of being a calibre is preserved under continuous mappings; every uncountable regular cardinal number is a calibre of any dyadic compactum. If the first uncountable cardinal number is a calibre of a space 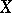 , then
, then 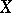 satisfies the Suslin condition. In some models of set theory the converse is almost true, namely, Martin's axiom and the condition
satisfies the Suslin condition. In some models of set theory the converse is almost true, namely, Martin's axiom and the condition 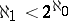 imply the following: If a space
imply the following: If a space 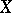 satisfies the Suslin condition, then every uncountable family of non-empty open sets in
satisfies the Suslin condition, then every uncountable family of non-empty open sets in 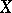 contains an uncountable centred subfamily. In particular, in this model, the cardinal number
contains an uncountable centred subfamily. In particular, in this model, the cardinal number 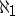 is a calibre for every compactum with the Suslin condition. In some other models of set theory, a compactum with the Suslin condition exists for which
is a calibre for every compactum with the Suslin condition. In some other models of set theory, a compactum with the Suslin condition exists for which 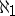 is not a calibre.
is not a calibre.
References
| [1] | N.A. Suslin, "On the product of topological spaces" Trudy. Mat. Inst. Steklov , 24 (1948) (In Russian) |
Comments
The spelling caliber is more common.
Usually, calibers are defined using indexed collections of open sets. In that case a cardinal number 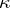 is a caliber of
is a caliber of 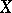 if and only if for every collection
if and only if for every collection 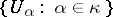 of non-empty open subsets of
of non-empty open subsets of 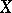 there is a set
there is a set 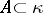 of size
of size 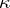 such that
such that 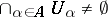 .
.
One also considers precalibers: a cardinal number 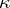 is a precaliber of
is a precaliber of 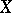 if and only if for every collection
if and only if for every collection 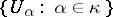 of non-empty subsets of
of non-empty subsets of 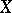 there is a set
there is a set 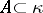 of size
of size 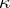 such that
such that 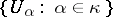 has the finite intersection property (i.e. the intersection of any finite number of
has the finite intersection property (i.e. the intersection of any finite number of 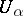 is non-empty). Thus, Martin's axiom (cf. Suslin hypothesis) plus the negation of the continuum hypothesis imply that every space satisfying the Suslin condition has
is non-empty). Thus, Martin's axiom (cf. Suslin hypothesis) plus the negation of the continuum hypothesis imply that every space satisfying the Suslin condition has 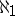 as a precaliber, while for a compact space its calibers and precalibers are the same.
as a precaliber, while for a compact space its calibers and precalibers are the same.
References
| [a1] | S. Argyros, A. Tsarpalias, "Calibers of compact spaces" Trans. Amer. Math. Soc. , 270 (1982) pp. 149–162 |
| [a2] | S. Broverman, J. Ginsburg, K. Kunen, F.D. Tall, "Topologies determined by 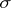 -ideals on -ideals on  " Canad. J. Math. , 30 (1978) pp. 1306–1312 " Canad. J. Math. , 30 (1978) pp. 1306–1312 |
| [a3] | W.W. Comfort, S. Negrepontis, "Chain conditions in topology" , Cambridge Univ. Press (1982) |
| [a4] | I. Juhász, "Cardinal functions. Ten years later" , MC Tracts , 123 , Math. Centre (1980) |
Calibre. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Calibre&oldid=17075