Burnside group
Let 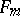 be a free group of rank
be a free group of rank 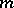 . The free
. The free 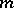 -generator Burnside group
-generator Burnside group 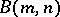 of exponent
of exponent  is defined to be the quotient group of
is defined to be the quotient group of  by the subgroup
by the subgroup 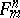 of
of  generated by all
generated by all  th powers of elements of
th powers of elements of 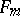 . Clearly,
. Clearly,  is the "largest"
is the "largest" 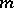 -generator group of exponent
-generator group of exponent  (that is, a group whose elements satisfy the identity
(that is, a group whose elements satisfy the identity 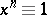 ) in the sense that if
) in the sense that if 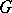 is an
is an 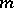 -generator group of exponent
-generator group of exponent  then there exists an epimorphism
then there exists an epimorphism 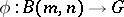 . In 1902, W. Burnside [a3] posed a problem (which later became known as the Burnside problem for periodic groups) that asks whether every finitely-generated group of exponent
. In 1902, W. Burnside [a3] posed a problem (which later became known as the Burnside problem for periodic groups) that asks whether every finitely-generated group of exponent  is finite, or, equivalently, whether the free Burnside groups
is finite, or, equivalently, whether the free Burnside groups 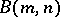 are finite (cf. also Burnside problem).
are finite (cf. also Burnside problem).
It is easy to show that the free  -generator Burnside group
-generator Burnside group 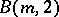 of exponent
of exponent  is an elementary Abelian 2-group and the order
is an elementary Abelian 2-group and the order  of
of 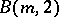 is
is 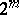 . Burnside showed that the groups
. Burnside showed that the groups 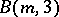 are finite for all
are finite for all 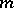 . In 1933, F. Levi and B.L. van der Waerden (see [a4]) proved that the Burnside group
. In 1933, F. Levi and B.L. van der Waerden (see [a4]) proved that the Burnside group 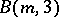 has the class of nilpotency equal to
has the class of nilpotency equal to  , when
, when  , and the order
, and the order 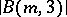 equals
equals 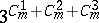 , where
, where 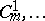 are binomial coefficients. In 1940, I.N. Sanov [a18] proved that the free Burnside groups
are binomial coefficients. In 1940, I.N. Sanov [a18] proved that the free Burnside groups 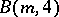 of exponent
of exponent 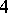 are also finite. In 1954, S.J. Tobin proved that
are also finite. In 1954, S.J. Tobin proved that 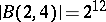 (see [a4]). By making use of computers, A.J. Bayes, J. Kautsky, and J.W. Wamsley showed in 1974 that
(see [a4]). By making use of computers, A.J. Bayes, J. Kautsky, and J.W. Wamsley showed in 1974 that 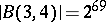 and W.A. Alford, G. Havas and M.F. Newman established in 1975 that
and W.A. Alford, G. Havas and M.F. Newman established in 1975 that 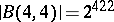 (see [a4]). It is also known (see [a4]) that the class of nilpotency of
(see [a4]). It is also known (see [a4]) that the class of nilpotency of 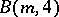 equals
equals  when
when  . On the other hand, in 1978, Yu.P. Razmyslov constructed an example of a non-solvable countable group of exponent
. On the other hand, in 1978, Yu.P. Razmyslov constructed an example of a non-solvable countable group of exponent 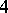 (see [a4]). In 1958, M. Hall [a8] proved that the Burnside groups
(see [a4]). In 1958, M. Hall [a8] proved that the Burnside groups 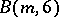 of exponent
of exponent  are finite and have the order given by the formula
are finite and have the order given by the formula 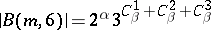 , where
, where 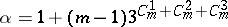 and
and 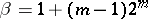 .
.
The attempts to approach the Burnside problem via finite groups gave rise to a restricted version of the Burnside problem (called the restricted Burnside problem) which was stated by W. Magnus [a14] in 1950 and asks whether there exists a number 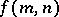 so that the order of any finite
so that the order of any finite 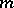 -generator group of exponent
-generator group of exponent  is less than
is less than 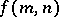 . The existence of such a bound
. The existence of such a bound 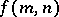 was proven for prime
was proven for prime  by A.I. Kostrikin [a11] in 1959 (see also [a12]) and for
by A.I. Kostrikin [a11] in 1959 (see also [a12]) and for 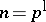 with a prime number
with a prime number 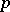 by E.I. Zel'manov [a19], [a20] in 1991–1992. It then follows from the Hall–Higman reduction results [a6] and the classification of finite simple groups that a bound
by E.I. Zel'manov [a19], [a20] in 1991–1992. It then follows from the Hall–Higman reduction results [a6] and the classification of finite simple groups that a bound  does exist for all
does exist for all  and
and  .
.
In 1968, P.S. Novikov and S.I. Adyan [a15] gave a negative solution to the Burnside problem for sufficiently large odd exponents by an explicit construction of infinite free Burnside groups 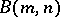 , where
, where 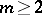 and
and  is odd,
is odd, 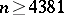 , by means of generators and defining relators. See [a15] for a powerful calculus of periodic words and a large number of lemmas, proved by simultaneous induction. Later, Adyan [a1] improved on the estimate for the exponent
, by means of generators and defining relators. See [a15] for a powerful calculus of periodic words and a large number of lemmas, proved by simultaneous induction. Later, Adyan [a1] improved on the estimate for the exponent  and brought it down to odd
and brought it down to odd 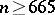 . Using their machinery, Novikov and Adyan obtained other results on the free Burnside groups
. Using their machinery, Novikov and Adyan obtained other results on the free Burnside groups  . In particular, the word and conjugacy problems were proved to be solvable for the presentations of
. In particular, the word and conjugacy problems were proved to be solvable for the presentations of 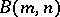 constructed in [a15], any Abelian or finite subgroup of
constructed in [a15], any Abelian or finite subgroup of  was shown to be cyclic (for these and other results, see [a1]; cf. also Identity problem; Conjugate elements).
was shown to be cyclic (for these and other results, see [a1]; cf. also Identity problem; Conjugate elements).
A much simpler construction of free Burnside groups 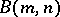 for
for 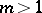 and odd
and odd  was given by A.Yu. Ol'shanskii [a16] in 1982 (see also [a17]). In 1994, further developing Ol'shanskii's geometric method, S.V. Ivanov [a9] constructed infinite free Burnside groups
was given by A.Yu. Ol'shanskii [a16] in 1982 (see also [a17]). In 1994, further developing Ol'shanskii's geometric method, S.V. Ivanov [a9] constructed infinite free Burnside groups 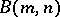 , where
, where  ,
, 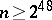 and
and  is divisible by
is divisible by 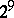 if
if  is even, thus providing a negative solution to the Burnside problem for almost all exponents.
is even, thus providing a negative solution to the Burnside problem for almost all exponents.
The construction of free Burnside groups 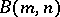 given in [a16], [a9] is based on the following inductive definitions. Let
given in [a16], [a9] is based on the following inductive definitions. Let 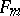 be a free group over an alphabet
be a free group over an alphabet 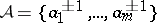 ,
,  , let
, let 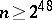 and let
and let  be divisible by
be divisible by 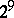 (from now on these restrictions on
(from now on these restrictions on 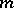 and
and  are assumed, unless otherwise stated; note that this estimate
are assumed, unless otherwise stated; note that this estimate 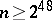 was improved on by I.G. Lysenok [a13] to
was improved on by I.G. Lysenok [a13] to 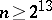 in 1996). By induction on
in 1996). By induction on 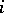 , let
, let 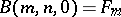 and, assuming that the group
and, assuming that the group 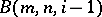 with
with  is already constructed as a quotient group of
is already constructed as a quotient group of 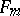 , define
, define 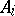 to be a shortest element of
to be a shortest element of 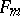 (if any) the order of whose image (under the natural epimorphism
(if any) the order of whose image (under the natural epimorphism 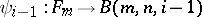 ) is infinite. Then
) is infinite. Then 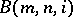 is constructed as a quotient group of
is constructed as a quotient group of 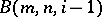 by the normal closure of
by the normal closure of 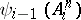 . Clearly,
. Clearly, 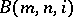 has a presentation of the form
has a presentation of the form 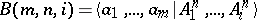 , where
, where 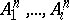 are the defining relators of
are the defining relators of  . It is proven in [a9] (and in [a16] for odd
. It is proven in [a9] (and in [a16] for odd 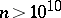 ) that for every
) that for every 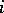 the word
the word 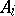 does exist. Furthermore, it is shown in [a9] (and in [a16] for odd
does exist. Furthermore, it is shown in [a9] (and in [a16] for odd  ) that the direct limit
) that the direct limit 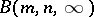 of the groups
of the groups 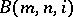 as
as 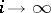 (obtained by imposing on
(obtained by imposing on 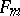 of relators
of relators 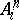 for all
for all 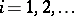 ) is exactly the free
) is exactly the free 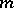 -generator Burnside group
-generator Burnside group  of exponent
of exponent  . The infiniteness of the group
. The infiniteness of the group 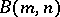 already follows from the existence of the word
already follows from the existence of the word 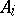 for every
for every 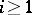 , since, otherwise,
, since, otherwise, 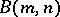 could be given by finitely many relators and so
could be given by finitely many relators and so 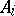 would fail to exist for sufficiently large
would fail to exist for sufficiently large 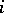 . It is also shown in [a9] that the word and conjugacy problems for the constructed presentation of
. It is also shown in [a9] that the word and conjugacy problems for the constructed presentation of  are solvable. In fact, these decision problems are effectively reduced to the word problem for groups
are solvable. In fact, these decision problems are effectively reduced to the word problem for groups 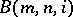 and it is shown that each
and it is shown that each 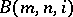 satisfies a linear isoperimetric inequality and hence
satisfies a linear isoperimetric inequality and hence  is a Gromov hyperbolic group [a5] (cf. Hyperbolic group).
is a Gromov hyperbolic group [a5] (cf. Hyperbolic group).
It should be noted that the structure of finite subgroups of the groups 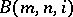 ,
, 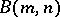 is very complex when the exponent
is very complex when the exponent  is even and, in fact, finite subgroups of
is even and, in fact, finite subgroups of 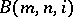 ,
, 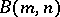 play a key role in proofs in [a9] (which, like [a15], also contains a large number of lemmas, proved by simultaneous induction). The central result related to finite subgroups of the groups
play a key role in proofs in [a9] (which, like [a15], also contains a large number of lemmas, proved by simultaneous induction). The central result related to finite subgroups of the groups 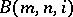 ,
,  is the following: Let
is the following: Let 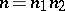 , where
, where 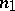 is the maximal odd divisor of
is the maximal odd divisor of  . Then any finite subgroup
. Then any finite subgroup 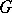 of
of 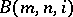 ,
, 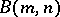 is isomorphic to a subgroup of the direct product
is isomorphic to a subgroup of the direct product 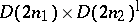 for some
for some 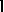 , where
, where 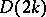 denotes a dihedral group of order
denotes a dihedral group of order  . The principal difference between odd and even exponents in the Burnside problem can be illustrated by pointing out that, on the one hand, for every odd
. The principal difference between odd and even exponents in the Burnside problem can be illustrated by pointing out that, on the one hand, for every odd 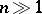 there are infinite
there are infinite  -generator groups of exponent
-generator groups of exponent  all of whose proper subgroups are cyclic (as was proved in [a2], see also [a17]) and, on the other hand, any
all of whose proper subgroups are cyclic (as was proved in [a2], see also [a17]) and, on the other hand, any  -group the orders of whose Abelian (or finite) subgroups are bounded is itself finite (see [a7]).
-group the orders of whose Abelian (or finite) subgroups are bounded is itself finite (see [a7]).
In 1997, Ivanov and Ol'shanskii [a10] showed that the above description of finite subgroups in 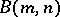 is complete (that is, every subgroup of
is complete (that is, every subgroup of  can actually be found in
can actually be found in 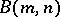 ) and obtained the following result: Let
) and obtained the following result: Let 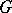 be a finite
be a finite  -subgroup of
-subgroup of 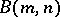 . Then the centralizer
. Then the centralizer 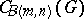 of
of 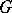 in
in 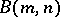 contains a subgroup
contains a subgroup 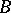 isomorphic to a free Burnside group
isomorphic to a free Burnside group 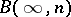 of infinite countable rank such that
of infinite countable rank such that  , whence
, whence 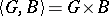 . (Since
. (Since 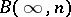 obviously contains subgroups isomorphic to both
obviously contains subgroups isomorphic to both 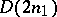 and
and 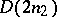 , an embedding of
, an embedding of 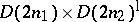 in
in  becomes trivial.) Among other results on subgroups of
becomes trivial.) Among other results on subgroups of 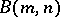 proven in [a10] are the following: The centralizer
proven in [a10] are the following: The centralizer  of a subgroup
of a subgroup 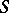 is infinite if and only if
is infinite if and only if 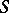 is a locally finite
is a locally finite  -group. Any infinite locally finite subgroup
-group. Any infinite locally finite subgroup 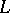 is contained in a unique maximal locally finite subgroup while any finite
is contained in a unique maximal locally finite subgroup while any finite  -subgroup is contained in continuously many pairwise non-isomorphic maximal locally finite subgroups. A complete description of infinite (maximal) locally finite subgroups of
-subgroup is contained in continuously many pairwise non-isomorphic maximal locally finite subgroups. A complete description of infinite (maximal) locally finite subgroups of 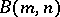 has also been obtained, in [a10].
has also been obtained, in [a10].
References
| [a1] | S.I. Adian, "The Burnside problems and identities in groups" , Springer (1979) (In Russian) |
| [a2] | V.S. Atabekian, S.V. Ivanov, "Two remarks on groups of bounded exponent" , 2243-B87 , VINITI, Moscow (1987) ((This is kept in the Depot of VINITI, Moscow, and is available upon request)) |
| [a3] | W. Burnside, "An unsettled question in the theory of discontinuous groups" Quart. J. Pure Appl. Math. , 33 (1902) pp. 230–238 |
| [a4] | N. Gupta, "On groups in which every element has finite order" Amer. Math. Monthly , 96 (1989) pp. 297–308 |
| [a5] | M. Gromov, "Hyperbolic groups" S.M. Gersten (ed.) , Essays in Group Theory , Springer (1987) pp. 75–263 |
| [a6] | Ph. Hall, G. Higman, "On the 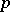 -length of -length of 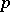 -soluble groups and reduction theorems for Burnside's problem" Proc. London Math. Soc. , 6 (1956) pp. 1–42 -soluble groups and reduction theorems for Burnside's problem" Proc. London Math. Soc. , 6 (1956) pp. 1–42 |
| [a7] | D. Held, "On abelian subgroups of an infinite  -group" Acta Sci. Math. (Szeged) , 27 (1966) pp. 97–98 -group" Acta Sci. Math. (Szeged) , 27 (1966) pp. 97–98 |
| [a8] | M. Hall Jr., "Solution of the Burnside problem for exponent 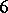 " Proc. Nat. Acad. Sci. USA , 43 (1957) pp. 751–753 " Proc. Nat. Acad. Sci. USA , 43 (1957) pp. 751–753 |
| [a9] | S.V. Ivanov, "The free Burnside groups of sufficiently large exponents" Internat. J. Algebra Comput. , 4 (1994) pp. 1–308 |
| [a10] | S.V. Ivanov, A.Yu. Ol'shanskii, "On finite and locally finite subgroups of free Burnside groups of large even exponents" J. Algebra , 195 (1997) pp. 241–284 |
| [a11] | A.I. Kostrikin, "On the Burnside problem" Math. USSR Izv. , 23 (1959) pp. 3–34 (In Russian) |
| [a12] | A.I. Kostrikin, "Around Burnside" , Nauka (1986) (In Russian) |
| [a13] | I.G. Lysenok, "Infinite Burnside groups of even period" Math. Ross. Izv. , 60 (1996) pp. 3–224 |
| [a14] | W. Magnus, "A connection between the Baker–Hausdorff formula and a problem of Burnside" Ann. Math. , 52 (1950) pp. 11–26 (Also: 57 (1953), 606) |
| [a15] | P.S. Novikov, S.I. Adian, "On infinite periodic groups I–III" Math. USSR Izv. , 32 (1968) pp. 212–244; 251–524; 709–731 |
| [a16] | A.Yu. Ol'shanskii, "On the Novikov–Adian theorem" Math. USSR Sb. , 118 (1982) pp. 203–235 (In Russian) |
| [a17] | A.Yu. Ol'shanskii, "Geometry of defining relations in groups" , Kluwer Acad. Publ. (1991) (In Russian) |
| [a18] | I.N. Sanov, "Solution of the Burnside problem for exponent 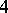 " Uch. Zapiski Leningrad State Univ. Ser. Mat. , 10 (1940) pp. 166–170 " Uch. Zapiski Leningrad State Univ. Ser. Mat. , 10 (1940) pp. 166–170 |
| [a19] | E.I. Zel'manov, "Solution of the restricted Burnside problem for groups of odd exponent" Math. USSR Izv. , 36 (1991) pp. 41–60 (In Russian) |
| [a20] | E.I. Zel'manov, "A solution of the restricted Burnside problem for  -groups" Math. USSR Sb. , 72 (1992) pp. 543–565 (In Russian) -groups" Math. USSR Sb. , 72 (1992) pp. 543–565 (In Russian) |
Burnside group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Burnside_group&oldid=19252