Burkill-Cesari integral
An extension of Burkill's integration process (for interval and rectangular functions; cf. Burkill integral) to set functions in abstract settings, introduced by L. Cesari in [a8], [a9]. It finds applications in the Weierstrass-type approach to the calculus of variations (see [a1], [a10], [a11], the survey [a2], and [a5], [a6], [a7]).
Elementary integration process for interval functions.
Given an interval 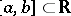 , let
, let 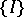 denote the collection of all closed subintervals. Let
denote the collection of all closed subintervals. Let  be the family of finite partitions
be the family of finite partitions 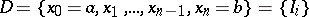 of
of  and let
and let 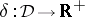 be the mesh function defined by
be the mesh function defined by 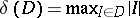 .
.
An interval function 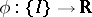 is said to be integrable if the limit
is said to be integrable if the limit 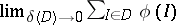 exists and is finite.
exists and is finite.
One of the main applications of this process is to the Jordan length of a continuous rectifiable curve 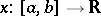 , which coincides with the integral of the function
, which coincides with the integral of the function 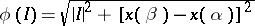 ,
, 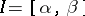 .
.
Burkill integration process for rectangle functions.
Given a closed rectangle 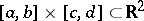 , let
, let 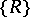 denote the collection of all closed subrectangles with sides parallel to the axes. Let
denote the collection of all closed subrectangles with sides parallel to the axes. Let 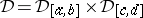 be the family of Cartesian subdivisions
be the family of Cartesian subdivisions 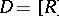 of
of 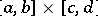 and let
and let 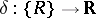 be the mesh function defined by
be the mesh function defined by 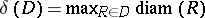 .
.
A rectangle function 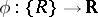 is said to be Burkill integrable if the limit
is said to be Burkill integrable if the limit
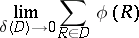 |
exists and is finite.
It has been proved that the area of a continuous surface of bounded variation coincides with the Burkill integral of a suitable rectangular function.
Burkill–Cesari integration process in an abstract setting.
Given a topological space 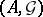 , let
, let 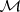 be the family of all subsets of
be the family of all subsets of 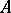 . Let
. Let 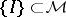 be a given class of sets, called "intervals" . A finite system
be a given class of sets, called "intervals" . A finite system 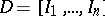 is a finite collection of non-overlapping intervals, i.e.
is a finite collection of non-overlapping intervals, i.e. 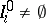 and
and 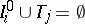 ,
,  ,
, 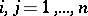 , where
, where 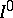 and
and 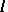 denote the
denote the  -interior and
-interior and 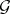 -closure, respectively.
-closure, respectively.
Let 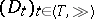 be a given net of finite systems and let
be a given net of finite systems and let 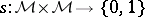 be the function defined by
be the function defined by 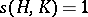 when
when 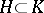 and
and 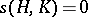 otherwise.
otherwise.
A function 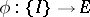 , where
, where  is a Banach space, is said to be Burkill–Cesari integrable over
is a Banach space, is said to be Burkill–Cesari integrable over  if the limit
if the limit
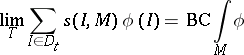 |
exists.
An efficient condition for the existence of the Burkill–Cesari integral is Cesari quasi-additivity: A function 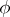 is said to be quasi-additive [a8] over
is said to be quasi-additive [a8] over 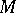 if for each
if for each 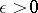 there exists a
there exists a  such that for every
such that for every 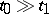 there exists a
there exists a  such that for every
such that for every 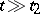 ,
,
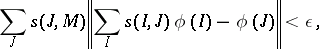 |
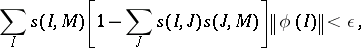 |
where 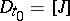 ,
, 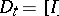 .
.
The function 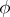 is said to be of bounded variation if
is said to be of bounded variation if  .
.
A quasi-additive function is Burkill–Cesari integrable. Moreover, if 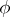 is quasi-additive and of bounded variation on
is quasi-additive and of bounded variation on 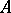 , then both functions
, then both functions 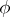 and
and 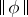 are quasi-additive on all subsets
are quasi-additive on all subsets 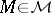 .
.
An analogous Burkill–Cesari weak integration process was introduced in [a3].
Subject to a suitable strengthening of the setting, the Burkill–Cesari integral admits extension to measures. Moreover, the total variation of the Burkill–Cesari measure of a function 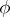 coincides with the Burkill–Cesari measure of
coincides with the Burkill–Cesari measure of 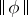 .
.
Connections of the Burkill–Cesari process with martingale theory were presented in [a4] (cf. also Martingale). A characterization of lower semicontinuity for Burkill–Cesari integrals was proposed in [a7]. The integration processes of Riemann, Lebesgue–Stieltjes, Hellinger, Bochner, Pettis, and Henstock can be regarded as particular Burkill–Cesari integrals (cf. also Riemann integral; Lebesgue–Stieltjes integral; Hellinger integral; Bochner integral; Pettis integral; Kurzweil–Henstock integral).
The variation, length and area of a curve or surface of bounded variation (not necessarily continuous) find a meaningful definition in terms of the Burkill–Cesari integral. Furthermore, a definition of weighted length and area can be introduced by means of this process.
More generally, the Burkill–Cesari integral has important applications in the definition of Weierstrass-type integrals in the calculus of variations (cf. Variational calculus). In fact the classical Lebesgue functionals are valid only with respect to Sobolev's variety, but the corresponding Weierstrass integrals provide a good and meaningful extension to the bounded variation setting.
References
| [a1] | J.C. Breckenridge, "Burkill–Cesari integrals of quasi additive interval functions" Pacific J. Math. , 37 (1971) pp. 635–654 |
| [a2] | C. Vinti, "Nonlinear integration and Weierstrass integral over a manifold: connections with theorems on martingales" J. Optimization Th. App. , 41 (1983) pp. 213–237 |
| [a3] | P. Brandi, A. Salvadori, "Sull'integrale debole alla Burkill–Cesari" Atti Sem. Mat. Fis. Univ. Modena , 23 (1978) pp. 14–38 |
| [a4] | P. Brandi, A. Salvadori, "Martingale ed integrale alla Burkill–Cesari" Atti Accad. Naz. Lincei , 67 (1979) pp. 197–203 |
| [a5] | P. Brandi, A. Salvadori, "A quasi-additive type condition and the integral over a BV variety" Pacific J. Math. , 146 (1990) pp. 1–19 |
| [a6] | P. Brandi, A. Salvadori, "On the non-parametric integral over a BV surface" J. Nonlinear Anal. , 13 (1989) pp. 1127–1137 |
| [a7] | P. Brandi, A. Salvadori, "On the semicontinuity of Burkill–Cesari integral" Rend. Circ. Mat. Palermo , 63 (1994) pp. 161–180 |
| [a8] | L. Cesari, "Quasi-additive set functions and the concept of integral over a variety" Trans. Amer. Math. Soc. , 102 (1962) pp. 94–113 |
| [a9] | Cesari,L, "Extension problem for quasi-additive set functions and Radon–Nykodym derivatives" Trans. Amer. Math. Soc. , 102 (1962) pp. 114–145 |
| [a10] | G. Warner, "The Burkill--Cesari integral" Duke Math. J , 35 (1968) pp. 61–78 |
| [a11] | G. Warner, "The generalized Weierstrass-type integral 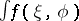 " Ann. Scuola Norm. Sup. Pisa , 22 (1968) pp. 163–191 " Ann. Scuola Norm. Sup. Pisa , 22 (1968) pp. 163–191 |
Burkill-Cesari integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Burkill-Cesari_integral&oldid=19041