Bukhvalov theorem
on kernel operators
The theory of kernel operators (cf. also Kernel of an integral operator) was essentially influenced by N. Dunford and B.J. Pettis [a2] around 1940. Other important results were obtained at about the same time by L.V. Kantorovich and B.Z. Vulikh. Among other results, it was shown that every bounded linear operator  ,
,  , is a kernel operator in the sense that there exists a measurable function
, is a kernel operator in the sense that there exists a measurable function  such that
such that  for almost all
for almost all  and
and  .
.
This result is known as Dunford's theorem. In the decades following these first results, kernel operators were intensively studied. While the first results were mainly concerned with a single kernel operator or were in the spirit of Dunford's theorem, the investigation of the structure of the space of all kernel operators in the space of all regular operators began in the 1960s, following the study of Banach function spaces (cf. also Banach function space), or even ideal spaces in the space of measurable functions.
Under very general assumptions it was shown that the kernel operators of  form a band in the space of all regular operators, where
form a band in the space of all regular operators, where  and
and  are ideals in the space of measurable functions
are ideals in the space of measurable functions 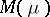 or
or 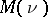 , respectively. At that time many properties of kernel operators were known. It was A.V. Bukhvalov who gave [a1] a simple characterization of kernel operators, as follows.
, respectively. At that time many properties of kernel operators were known. It was A.V. Bukhvalov who gave [a1] a simple characterization of kernel operators, as follows.
Let 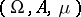 ,
,  be measure spaces (cf. also Measure space), let
be measure spaces (cf. also Measure space), let 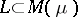 and
and 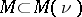 be ideals such that the support of the Köthe dual
be ideals such that the support of the Köthe dual 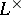 is all of
is all of  . Then for every linear operator
. Then for every linear operator  the following conditions are equivalent:
the following conditions are equivalent:
i) 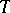 is a kernel operator.
is a kernel operator.
ii) If 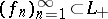 is an order-bounded sequence which is star convergent, then the sequence
is an order-bounded sequence which is star convergent, then the sequence 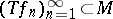 is convergent almost everywhere. Here, a sequence
is convergent almost everywhere. Here, a sequence  said to be star convergent to some
said to be star convergent to some 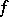 if every subsequence of the sequence
if every subsequence of the sequence 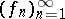 contains a subsequence
contains a subsequence  such that
such that 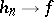 almost everywhere as
almost everywhere as 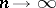 . Consequently,
. Consequently, 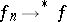 , as
, as 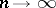 , if and only if
, if and only if  in the measure
in the measure  on every subset of finite measure.
on every subset of finite measure.
While the proof of i)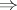 ii) is a simple consequence of the Lebesgue convergence theorem (cf. also Lebesgue theorem), the proof of ii)
ii) is a simple consequence of the Lebesgue convergence theorem (cf. also Lebesgue theorem), the proof of ii)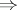 i) requires many results concerning the structure of the space of kernel operators in the space of all regular operators. A simplified version of the proof is due to A.R. Schep [a4].
i) requires many results concerning the structure of the space of kernel operators in the space of all regular operators. A simplified version of the proof is due to A.R. Schep [a4].
Bukhvalov's theorem is a powerful tool in the study of operators between Banach function spaces. In particular, his characterization of kernel operators leads to simple proofs of many classical results, such as Dunford's theorem and generalizations of it. For more information, see [a3], Sect. 3.3, or [a5].
References
| [a1] | A.V. Bukhvalov, "Integral representations of linear operators" J. Soviet Math. , 8 (1978) pp. 129–137 |
| [a2] | N. Dunford, J.B. Pettis, "Linear operators on summable functions" Trans. Amer. Math. Soc. , 47 (1940) pp. 323–392 |
| [a3] | P. Meyer-Nieberg, "Banach lattices" , Springer (1991) |
| [a4] | A.R. Schep, "Kernel operators" PhD Thesis Univ. Leiden (1977) |
| [a5] | A.C. Zaanen, "Riesz spaces" , II , North-Holland (1983) |
Bukhvalov theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bukhvalov_theorem&oldid=17381