Brownian local time
Let $W = \{ W _ { t } : t \geq 0 \}$ be a standard Wiener process (or, in other words, Brownian motion) living on $\mathbf{R}$ and started at $0$. The random set $\mathcal{Z} _ { 0 } : = \{ t : W _ { t } = 0 \}$, the so-called zero set of the Brownian path, is almost surely perfect (i.e. closed and dense in itself), unbounded and of Lebesgue measure $0$. The complement of $\mathcal{ Z}_ { 0 }$ is a countable union of open intervals.
A remarkable result of P. Lévy ([a6], [a7]) is that there exists a non-decreasing (random) function determined by $\mathcal{ Z}_ { 0 }$ which is constant on the open intervals in the complement of $\mathcal{ Z}_ { 0 }$ and which has every point in $\mathcal{ Z}_ { 0 }$ as a (left and/or right) strict increase point. This function is called the Brownian local time (at $0$). It is clear that a similar construction can be made at any point $x$.
The existence of the local time can be deduced from the fact (also due to Lévy) that the processes $W ^ { + } : = \{ | W _ { t } | : t \geq 0 \}$ and $W ^ { o } : = \{ M _ { t } - W _ { t } : t \geq 0 \}$, where $M _ { t } : = \operatorname { sup } _ { s \leq t } W _ { s }$, are identical in law. Indeed, for $W ^ { \circ }$ the function $t \mapsto M _ { t }$ has the desired properties of local time; for the proof that $M _ { t }$, for a given $t$, is determined by $\mathcal{Z} _ { 0 } ^ { o } ( t ) : = \{ s : M _ { s } - W _ { s } = 0 , s \leq t \}$, see [a4]. Because $W ^ { + }$ and $W ^ { \circ }$ are identical in law, there exists a function with corresponding properties connected to $W ^ { + }$.
Let ${\bf l} ( t , x )$ be the Brownian local time at $x$ at time $t$. Then almost surely
\begin{equation*} {\bf l} ( t , x ) = \operatorname { lim } _ { \epsilon \rightarrow 0 } \frac { 1 } { 2 \varepsilon } \int _ { 0 } ^ { t } 1_{( x - \varepsilon , x + \varepsilon )} ( W _ { s } ) d s, \end{equation*}
and this leads to the occupation-time formula
\begin{equation*} \int _ { 0 } ^ { t } f ( W _ { s } ) d s = \int \operatorname{l}( t , x ) f ( x ) d x, \end{equation*}
where $f$ is a Borel-measurable function (cf. also Borel function).
As seen above, $\mathbf{l} ( t , 0 )$ can be viewed as the measure of the zero set $\mathcal{Z} _ { 0 } \cap [ 0 , t] $. In fact, it has been proved in [a11] and [a9] that 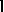 is the random Hausdorff $l$-measure (cf. also Hausdorff measure) of $\mathcal{Z} _ { 0 } \cap [ 0 , t] $ with $l ( u ) = ( 2 u | \operatorname {ln} | \operatorname {ln} u | | ) ^ { 1 / 2 }$.
is the random Hausdorff $l$-measure (cf. also Hausdorff measure) of $\mathcal{Z} _ { 0 } \cap [ 0 , t] $ with $l ( u ) = ( 2 u | \operatorname {ln} | \operatorname {ln} u | | ) ^ { 1 / 2 }$.
Introduce for $x > 0$ the right-continuous inverse of $M$ by
\begin{equation*} \tau _ { x } : = \operatorname { inf } \{ s : M _ { s } > x \}. \end{equation*}
By the strong Markov property (cf. Markov property) and spatial homogeneity of Brownian motion, the process $\tau : = \{ \tau _ { x } : x \geq 0 \}$ is increasing and has independent and identically distributed increments, in other words, $\tau$ is a subordinator. Because $\mathbf{l} ( t , 0 )$ and $M _ { t }$ are, for every $t \geq 0$, identical in law, also the so-called inverse local time
\begin{equation*} \alpha _ { x } : = \operatorname { inf } \{ s : \operatorname{l} ( s , 0 ) > x \} \end{equation*}
and $\tau_x$ are identical in law. Hence, the finite-dimensional distributions of $\alpha$ are determined by the Laplace transform
\begin{equation*} \mathsf{E} ( \operatorname { exp } ( - u \alpha _ { x } ) ) = \end{equation*}
\begin{equation*} = \operatorname { exp } \left( - x \int _ { 0 } ^ { \infty } ( 1 - e ^ { - u v } ) \frac { 1 } { \sqrt { 2 \pi v ^ { 3 } } } d v \right) = \end{equation*}
\begin{equation*} = \operatorname { exp } ( - x \sqrt { 2 u } ). \end{equation*}
The mapping $( t , x ) \mapsto \text{l} ( t , x )$, $t \geq 0$, $X \in \mathbf R$, is continuous. This is due to H.F. Trotter [a12]; for a proof based on the Itô formula, see, e.g., [a3].
The behaviour of the process $\{ \operatorname {l} ( T , x ) : x \in \mathbf R \}$ can be characterized for some stopping times $T$ (for first hitting times, for instance; cf. also Stopping time). Results in this direction are called Ray–Knight theorems [a10], [a5]; see also [a2].
The process $\{ \text{l} ( t , 0 ) : t \geq 0 \}$ is an example of an additive functional of Brownian motion having support at one point (i.e. at $0$). As such it is unique up to a multiplicative constant. See [a1].
Brownian local time is an important concept both in the theory and in applications of stochastic processes. It can be used, e.g., to construct diffusions from Brownian motion via random time change and to analyze stochastic differential equations (cf. also Stochastic differential equation). There are some natural problems in stochastic optimal control (finite fuel problem) and in financial mathematics (barrier options), for instance, where (Brownian) local time plays a crucial role.
For a survey article, see [a8].
References
| [a1] | R.M. Blumenthal, R.K. Getoor, "Markov processes and potential theory" , Acad. Press (1968) |
| [a2] | A.N. Borodin, P. Salminen, "Handbook of Brownian motion: Facts and formulae" , Birkhäuser (1996) |
| [a3] | N. Ikeda, S. Watanabe, "Stochastic differential equations and diffusion processes" , North-Holland &Kodansha (1981) |
| [a4] | K. Itô, H.P. McKean, "Diffusion processes and their sample paths" , Springer (1974) |
| [a5] | F. Knight, "Random walks and a sojourn density process of Brownian motion" Trans. Amer. Math. Soc. , 109 (1963) pp. 56–86 |
| [a6] | P. Lévy, "Processus stochastiques et mouvement brownien" , Gauthier-Villars (1948) |
| [a7] | P. Lévy, "Sur certains processus stochastiques homogénes" Compositio Math. , 7 (1939) pp. 283–339 |
| [a8] | H.P. McKean, "Brownian local time" Adv. Math. , 15 (1975) pp. 91–111 |
| [a9] | E. Perkins, "The exact Hausdorff measure of the level sets of Brownian motion" ZWvG , 58 (1981) pp. 373–388 |
| [a10] | D.B. Ray, "Sojourn times of a diffusion process Ill" J. Math. , 7 (1963) pp. 615–630 |
| [a11] | S.J. Taylor, J.G. Wendel, "The exact Hausdorff measure of the zero set of a stable process" ZWvG , 6 (1966) pp. 170–180 |
| [a12] | H.F. Trotter, "A property of Brownian motion paths. Ill" J. Math. , 2 (1958) pp. 425–433 |
Brownian local time. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brownian_local_time&oldid=50741