Brouwer degree
topological degree
A fundamental concept in algebraic topology, differential topology and mathematical analysis. It is rooted in the fundamental work of L. Kronecker [a5] for systems of smooth real-valued functions  of
of  real variables such that
real variables such that  is a regular value for
is a regular value for  ,
,  is bounded and the
is bounded and the  do not vanish simultaneously on
do not vanish simultaneously on  . Letting
. Letting  , Kronecker showed in 1869 that the number
, Kronecker showed in 1869 that the number  defined (in modern notation) by the integral
defined (in modern notation) by the integral
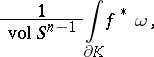 |
where 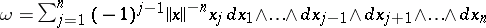 , is equal to
, is equal to  , when this sum makes sense, i.e. when the Jacobian of
, when this sum makes sense, i.e. when the Jacobian of 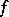 does not vanish on
does not vanish on 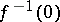 (cf. also Jacobian). The special case when
(cf. also Jacobian). The special case when 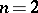 and
and  is a closed simple curve was already considered by A. Cauchy in 1837 (the winding number). After several interesting applications to differential equations and function theory by H. Poincaré in 1882–1886 and P.G. Bohl in 1904, in 1910–1912, L.E.J. Brouwer [a2] and J. Hadamard [a3] made this Kronecker integral a topological tool by extending it to continuous mappings
is a closed simple curve was already considered by A. Cauchy in 1837 (the winding number). After several interesting applications to differential equations and function theory by H. Poincaré in 1882–1886 and P.G. Bohl in 1904, in 1910–1912, L.E.J. Brouwer [a2] and J. Hadamard [a3] made this Kronecker integral a topological tool by extending it to continuous mappings  and more general sets
and more general sets 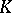 . Hadamard refined Kronecker's analytical approach, but Brouwer created and used new simplicial techniques to define a (global) degree
. Hadamard refined Kronecker's analytical approach, but Brouwer created and used new simplicial techniques to define a (global) degree 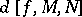 for continuous mappings
for continuous mappings 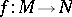 between two oriented compact boundaryless connected manifolds of the same finite dimension. He used it to prove the theorems on invariance of dimension and invariance of domain (cf. also Brouwer theorem). Kronecker's integral can be seen as a special case of the Brouwer degree
between two oriented compact boundaryless connected manifolds of the same finite dimension. He used it to prove the theorems on invariance of dimension and invariance of domain (cf. also Brouwer theorem). Kronecker's integral can be seen as a special case of the Brouwer degree 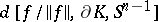 , or of the (local) Brouwer degree
, or of the (local) Brouwer degree 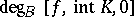 , defined as follows (cf. also Degree of a mapping).
, defined as follows (cf. also Degree of a mapping).
If 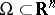 is open and bounded, the Brouwer degree
is open and bounded, the Brouwer degree 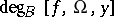 of a continuous mapping
of a continuous mapping 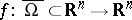 can be defined for each
can be defined for each  using an approximation scheme introduced by M. Nagumo [a8] in 1950. The idea consists in defining it first for
using an approximation scheme introduced by M. Nagumo [a8] in 1950. The idea consists in defining it first for 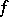 smooth and
smooth and 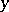 a regular value of
a regular value of 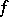 , through the formula
, through the formula
 |
and then to approximate the continuous function  and the point
and the point 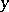 above by a sequence of such functions and points for which this definition holds. This is possible by the Weierstrass approximation theorem (cf. Weierstrass theorem) and the Sard theorem. The degrees of the approximations stabilize to a common value, denoted by
above by a sequence of such functions and points for which this definition holds. This is possible by the Weierstrass approximation theorem (cf. Weierstrass theorem) and the Sard theorem. The degrees of the approximations stabilize to a common value, denoted by  and being an algebraic count of the number of counter-images of
and being an algebraic count of the number of counter-images of 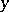 under
under 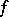 in
in  , which is stable for small perturbations of
, which is stable for small perturbations of  and
and 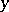 . A similar approach can be used to define
. A similar approach can be used to define  when
when 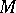 and
and 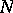 are oriented boundaryless differentiable manifolds.
are oriented boundaryless differentiable manifolds.
Properties and axiomatic characterization.
The first basic property of the Brouwer degree is its additivity-excision: if 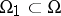 and
and  are disjoint open subsets such that
are disjoint open subsets such that 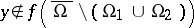 , then one has
, then one has 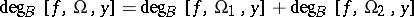 .
.
The second property is its homotopy invariance: let 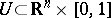 be a bounded open set,
be a bounded open set, 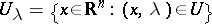 , let
, let 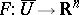 be continuous, and let
be continuous, and let 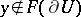 ; then
; then  is independent of
is independent of 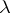 .
.
It has been shown in the 1970s (see [a9] for references) that the Brouwer degree can be uniquely characterized as the integer-valued function 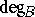 on the set
on the set
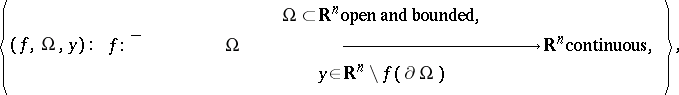 |
by the additivity-excision and the homotopy invariance properties, together with the following direct consequence of the definition (the normalization property): if 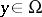 , then
, then 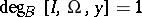 .
.
The additivity-excision property implies the existence property: if 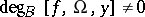 , then
, then 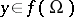 .
.
Easy consequences of the homotopy invariance are the equalities  when
when 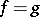 on
on 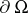 , and
, and  when
when  and
and  belong to the same component
belong to the same component 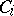 of
of 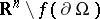 (with the common value written
(with the common value written  ).
).
The existence and homotopy properties have many important applications in studying the existence and bifurcation of solutions of various types of equations.
Product theorem.
In 1934, J. Leray [a6] proved a useful product theorem for the Brouwer degree: let 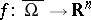 and
and 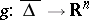 , with
, with 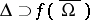 , be continuous functions such that
, be continuous functions such that  . Denoting by
. Denoting by 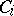 the bounded components of
the bounded components of 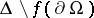 , one has
, one has 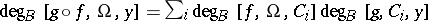 , where only finitely many terms are different from zero.
, where only finitely many terms are different from zero.
This result has deep applications in topology, for example the Jordan separation theorem: for homeomorphic compact subsets  and
and 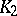 of
of 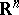 , the sets
, the sets 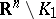 and
and 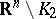 have the same number of connected components.
have the same number of connected components.
Fixed-point theorems.
An easy consequence of the Brouwer degree is the following Knaster–Kuratowski–Mazurkiewicz fixed-point theorem, first stated and proved in 1929 [a4]: let 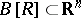 be the closed ball of centre
be the closed ball of centre  and radius
and radius  and let
and let  be a continuous function such that
be a continuous function such that 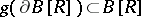 . Then there is at least one
. Then there is at least one 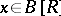 such that
such that 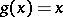 .
.
The special case where 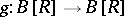 is the Brouwer fixed-point theorem [a2], which has many different and useful equivalent forms.
is the Brouwer fixed-point theorem [a2], which has many different and useful equivalent forms.
Degree of symmetric mappings.
Useful computational results hold under symmetry assumptions. The oldest one, which corresponds to 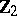 -symmetry, was conjectured by S.M. Ulam and proved by K. Borsuk in 1933 [a1]: let
-symmetry, was conjectured by S.M. Ulam and proved by K. Borsuk in 1933 [a1]: let  be a bounded open symmetric neighbourhood of the origin in
be a bounded open symmetric neighbourhood of the origin in 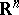 and let
and let 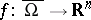 be a continuous odd function such that
be a continuous odd function such that 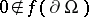 ; then
; then 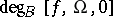 is odd.
is odd.
This result and its more recent 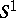 -version are basic in critical point theory [a7].
-version are basic in critical point theory [a7].
Other approaches and extensions.
The Brouwer degree is a very versatile concept which can be defined through techniques of algebraic topology, differential topology or algebraic geometry. For example, if  is continuous and
is continuous and 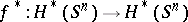 is the induced homomorphism on the homology groups of
is the induced homomorphism on the homology groups of 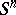 over
over  (cf. also Homology group), then
(cf. also Homology group), then  is isomorphic to
is isomorphic to 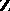 and hence
and hence 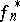 becomes multiplication by an integer, which is
becomes multiplication by an integer, which is 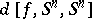 . If
. If  is any continuous extension of
is any continuous extension of 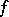 to the closed unit ball
to the closed unit ball 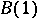 , then
, then 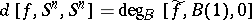 .
.
In 1995, H. Brézis and L. Nirenberg [a10], [a11] defined a Brouwer degree for certain not necessarily continuous mappings  belonging to a Sobolev or other function space.
belonging to a Sobolev or other function space.
Extensions of the Brouwer degree to various classes of mappings between infinite-dimensional spaces are also known. The most fundamental one is the Leray–Schauder degree, defined in 1934 for compact perturbations of the identity defined on the closure of a bounded open subset of a normed vector space (cf. also Degree of a mapping).
References
| [a1] | K. Borsuk, "Drei Sätze über die  -dimensionale euklidische Sphäre" Fundam. Math. , 21 (1933) pp. 177–190 -dimensionale euklidische Sphäre" Fundam. Math. , 21 (1933) pp. 177–190 |
| [a2] | L.E.J. Brouwer, "Ueber Abbildungen von Mannigfaltigkeiten" Math. Ann. , 71 (1912) pp. 97–115 |
| [a3] | J. Hadamard, "Sur quelques applications de l'indice de Kronecker" J. Tannery (ed.) , Introduction à la théorie des fonctions d'une variable , 2 , Hermann (1910) pp. 875–915 |
| [a4] | B. Knaster, C. Kuratowski, S. Mazurkiewicz, "Ein Beweis des Fixpunktsatzes für  -dimensionale Simplexe" Fundam. Math. , 14 (1929) pp. 132–137 -dimensionale Simplexe" Fundam. Math. , 14 (1929) pp. 132–137 |
| [a5] | L. Kronecker, "Ueber Systeme von Funktionen mehrerer Variabeln" Monatsber. Berlin Akad. (1869) pp. 159–193; 688–698 |
| [a6] | J. Leray, "Topologie des espaces abstraits de M. Banach" C.R. Acad. Sci. Paris , 200 (1935) pp. 1082–1084 |
| [a7] | J. Mawhin, M. Willem, "Critical point theory and Hamiltonian systems" , Springer (1989) |
| [a8] | M. Nagumo, "A theory of degree of mapping based on infinitesimal analysis" Amer. J. Math. , 73 (1951) pp. 485–496 |
| [a9] | E. Zeidler, "Nonlinear functional analysis and its applications" , I , Springer (1986) |
| [a10] | H. Brézis, L. Nirenberg, "Degree theory and BMO" Selecta Math. , 1 (1995) pp. 197–263 |
| [a11] | H. Brézis, L. Nirenberg, "Degree theory and BMO" Selecta Math. , 2 (1996) pp. 1–60 |
Brouwer degree. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brouwer_degree&oldid=13548