Borel subgroup
A maximal connected solvable algebraic subgroup of a linear algebraic group 
. Thus, for instance, the subgroup of all non-singular upper-triangular matrices is a Borel subgroup in the general linear group 
. A. Borel [1] was the first to carry out a systematic study of maximal connected solvable subgroups of algebraic groups. Borel subgroups can be characterized as minimal parabolic subgroups, i.e. algebraic subgroups 
of the group 
for which the quotient variety 
is projective. All Borel subgroups of 
are conjugate and, if the Borel subgroups 
, 
and the group 
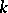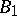are defined over a field 
, 
and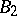 
are conjugate by an element of 
. The intersection of any two Borel subgroups of a group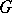 
contains a maximal torus of 
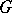; if this intersection is a maximal torus, such Borel subgroups are said to be opposite. Opposite Borel subgroups exist in 
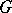if and only if 
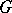is a reductive group. If 
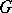is connected, it is the union of all its Borel subgroups, and any parabolic subgroup coincides with its normalizer in 
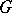. In such a case a Borel subgroup is maximal among all (and not only algebraic and connected) solvable subgroups of 
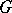. Nevertheless, maximal solvable subgroups in 
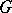which are not Borel subgroups usually exist. The commutator subgroup of a Borel subgroup 
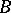coincides with its unipotent part 
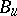, while the normalizer of 
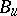in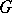 
coincides with 
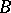. If the characteristic of the ground field is 0, and 
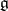is the Lie algebra of 
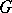, then the subalgebra 
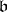of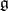 
which is the Lie algebra of the Borel subgroup 
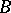of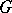 
is often referred to as a Borel subalgebra in 
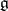. The Borel subalgebras in 
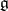are its maximal solvable subalgebras. If 
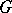is defined over an arbitrary field 
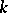, the parabolic subgroups which are defined over 
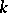and are minimal for this property, play a role in the theory of algebraic groups over 
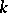similar to that of the Borel groups. For example, two such parabolic subgroups are conjugate by an element of 
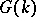[2].
References
| [1] | A. Borel, "Groupes linéaires algébriques" Ann. of Math. (2) , 64 : 1 (1956) pp. 20–82 |
| [2] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 |
Borel subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_subgroup&oldid=14476