Bohnenblust theorem

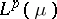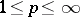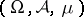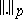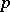Consider the space , , and a measure space . Since the norm is -additive, it is easily seen that the following condition is satisfied: For all 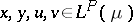satisfying 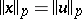, , 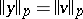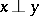and 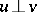(in the sense of disjoint support), one has .

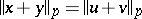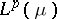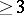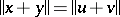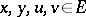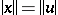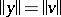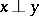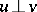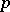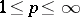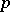In [a2] H.F. Bohnenblust showed that the spaces are the only Banach lattices (cf. also Banach lattice) possessing this property; more precisely, he proved the following theorem, now known as the Bohnenblust theorem: Let be a Banach lattice of dimension satisfying for all such that , , , and . Then there exists a , , such that the norm on is -additive.

Here, for 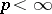, a norm is said to be 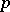-additive if 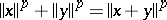for all 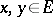with 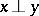; a norm is said to be 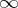-additive, or, equivalently, 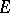is said to be an 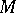-space, if 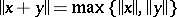for all 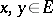with .

It should be noted that when 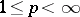, every Banach lattice with a -additive norm is isometrically isomorphic to 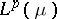, with 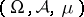a suitable measure space. This representation theorem is essentially due to S. Kakutani [a3], who considered the case 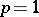; the proof of the more general result follows almost the same lines. For 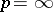the situation is not so clear: there exist many 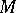-spaces that are not isomorphic to any concrete 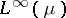-space, for instance .

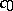In the proof of his theorem, H.F. Bohnenblust introduced an interesting and tricky method to construct the 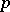such that the norm is 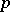-additive. A similar method was used later by M. Zippin [a5] to characterize 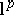-spaces in terms of bases. Since the proof given by Bohnenblust is interesting in itself, the main ideas are sketched below.

By hypothesis, there exists a function 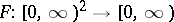defined by

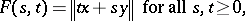whenever and 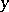are disjoint vectors of norm one. It can easily be verified that the function has the following properties:

1) ;

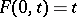ii) ;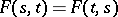

iii) ;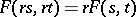

iv) ;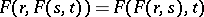

v) 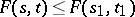if 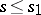, . The only non-trivial inclusion iv) follows from

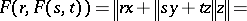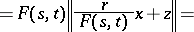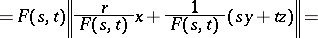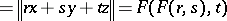for all disjoint 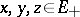of norm one and 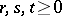with .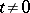

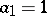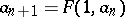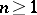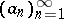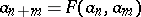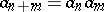One defines and for all . Property v) implies that the sequence is increasing. By induction one obtains and . If 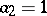, then properties i)–v) easily imply 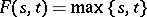for all 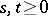. Hence, 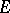is an 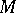-space.

Assume now that 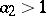and let 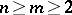. For all 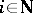there exists a 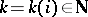such that 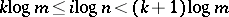. Since 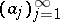is an increasing sequence, one concludes from 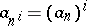that or, equivalently, that 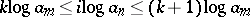. This yields

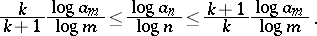Letting ,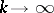

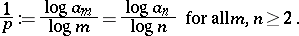It is clear that 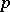does not depend on the special choice of 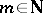. Moreover, 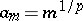for all 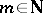. Since 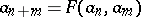, it follows that 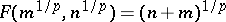for all 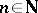. Consequently,

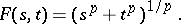From 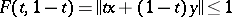for all 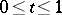it follows that 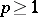. This completes the proof.

Bohnenblust's theorem has some interesting consequences. For instance, T. Ando [a1] used it to prove that a Banach lattice 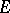is isometrically isomorphic to 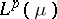for some measure space 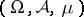, or to some 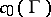, if and only if every closed sublattice of 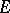is the range of a positive contractive projection.

References

[a1]	T. Ando, "Banachverbände und positive Projektionen" Math. Z. , 109 (1969) pp. 121–130
[a2]	H.F. Bohnenblust, "An axiomatic characterization of 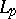-spaces" Duke Math. J. , 6 (1940) pp. 627–640
[a3]	S. Kakutani, "Concrete representation of abstract 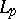-spaces and the mean ergodic theorem" Ann. of Math. , 42 (1941) pp. 523–537
[a4]	P. Meyer-Nieberg, "Banach lattices" , Springer (1991)
[a5]	M. Zippin, "On perfectly homogeneous bases in Banach spaces" Israel J. Math. , 4 A (1966) pp. 265–272