Bochner-Riesz means
Bochner–Riesz averages
Bochner–Riesz means can be defined and developed in different settings: multiple Fourier integrals; multiple Fourier series; other orthogonal series expansions. Below these three separate cases will be pursued, with regard to 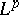 -convergence, almost-everywhere convergence, localization, and convergence or oscillation at a pre-assigned point.
-convergence, almost-everywhere convergence, localization, and convergence or oscillation at a pre-assigned point.
A primary motivation for studying these operations lies in the fact that a general Fourier series or Fourier integral expansion can only be expected to converge in the sense of the mean square (i.e., 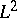 ) norm; by inserting various smoothing and convergence factors, the convergence can often be improved to
) norm; by inserting various smoothing and convergence factors, the convergence can often be improved to 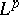 ,
, 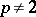 , or to the almost-everywhere sense.
, or to the almost-everywhere sense.
If 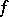 is an integrable function on a Euclidean space
is an integrable function on a Euclidean space  , with Fourier transform
, with Fourier transform  , the Bochner–Riesz means of order
, the Bochner–Riesz means of order  are defined by:
are defined by:
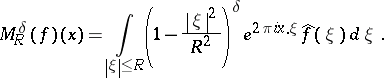 |
This also can be formally written as a convolution with a kernel function. If 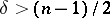 (the critical index), then this kernel is integrable; in particular,
(the critical index), then this kernel is integrable; in particular, 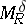 is a bounded operator on
is a bounded operator on 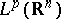 ,
, 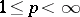 , and
, and 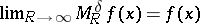 for almost every
for almost every  and
and 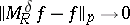 . Below the critical index, one has the following results:
. Below the critical index, one has the following results:
If 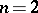 and
and 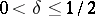 , then
, then 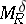 is a bounded operator on
is a bounded operator on 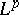 if and only if
if and only if 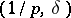 lies in the trapezoidal region defined by the inequalities
lies in the trapezoidal region defined by the inequalities 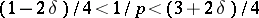 .
.
If 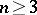 and
and  , then
, then 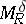 is a bounded operator on
is a bounded operator on 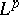 if and only if
if and only if 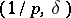 lies in the trapezoidal region defined by the inequalities
lies in the trapezoidal region defined by the inequalities 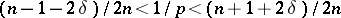 .
.
If  and
and 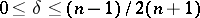 , then
, then 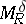 is a bounded operator on
is a bounded operator on 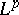 if
if  lies in the triangular region defined by the inequalities
lies in the triangular region defined by the inequalities 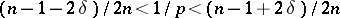 and is an unbounded operator if either
and is an unbounded operator if either 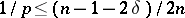 or
or 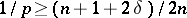 .
.
For any 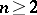 , in the limiting case
, in the limiting case 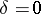 ,
,  is a bounded operator on
is a bounded operator on  if and only if
if and only if 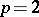 . If
. If 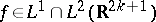 and
and 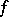 has
has 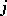 continuous derivatives, then
continuous derivatives, then 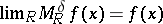 provided that
provided that 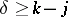 . If
. If 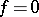 in an open ball centred at
in an open ball centred at  , then
, then 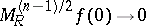 when
when 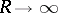 . There is also a Gibbs phenomenon for
. There is also a Gibbs phenomenon for 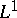 functions which have a simple jump across a hypersurface
functions which have a simple jump across a hypersurface 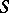 with respect to
with respect to 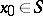 . If
. If 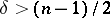 , then the set of accumulation points of
, then the set of accumulation points of 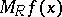 when
when 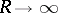 ,
, 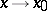 equals the segment with centre
equals the segment with centre 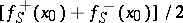 and length
and length 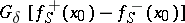 , where
, where 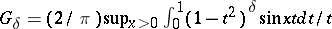 .
.
If 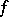 is an integrable function on the torus
is an integrable function on the torus 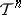 , the Bochner–Riesz means of order
, the Bochner–Riesz means of order 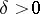 are defined by
are defined by
 |
where the Fourier coefficient is defined by 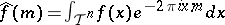 . If
. If 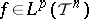 , then
, then
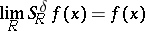 |
almost everywhere if 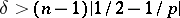 ; convergence in
; convergence in 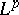 holds if
holds if 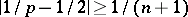 and
and  ,
, 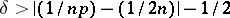 . If
. If 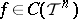 ,
, 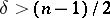 , then
, then 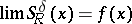 uniformly for
uniformly for 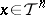 . At the critical index, one has the following behaviour: for any open ball centred at
. At the critical index, one has the following behaviour: for any open ball centred at  , there exists an
, there exists an 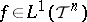 so that
so that 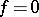 in the ball and
in the ball and 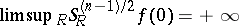 . There exists an integrable function
. There exists an integrable function 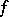 for which
for which 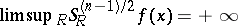 for almost every
for almost every 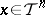 . If, in addition,
. If, in addition, 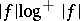 is integrable and
is integrable and 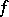 satisfies a Dini condition (cf. also Dini criterion) at
satisfies a Dini condition (cf. also Dini criterion) at 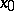 , then
, then 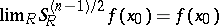 .
.
Bochner–Riesz means can be defined with respect to any orthonormal basis 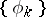 of the Hilbert space corresponding to a self-adjoint differential operator
of the Hilbert space corresponding to a self-adjoint differential operator 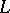 with eigenvalues
with eigenvalues 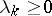 . In this setting, the Bochner–Riesz means of order
. In this setting, the Bochner–Riesz means of order 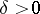 are defined by
are defined by
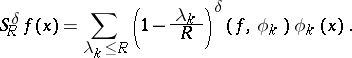 |
In the case of multiple Hermite series corresponding to the differential operator 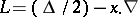 on
on 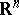 , one has
, one has 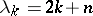 and the convergence in
and the convergence in 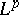 holds if
holds if 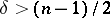 ; almost-everywhere convergence holds if
; almost-everywhere convergence holds if 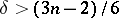 . In the case of an arbitrary elliptic differential operator on a compact manifold, it is known that if
. In the case of an arbitrary elliptic differential operator on a compact manifold, it is known that if 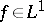 , then
, then  whenever
whenever 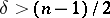 . For second-order operators there is an
. For second-order operators there is an 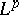 convergence theorem, provided that
convergence theorem, provided that 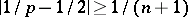 and
and 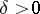 and
and 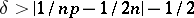 .
.
References
| [a1] | S. Bochner, "Summation of multiple Fourier series by spherical means" Trans. Amer. Math. Soc. , 40 (1936) pp. 175–207 |
| [a2] | C. Fefferman, "A note on spherical summation multipliers" Israel J. Math. , 15 (1973) pp. 44–52 |
| [a3] | B.I. Golubov, "On Gibb's phenomenon for Riesz spherical means of multiple Fourier integrals and Fourier series" Anal. Math. , 4 (1978) pp. 269–287 |
| [a4] | B.M. Levitan, "Ueber die Summierung mehrfacher Fourierreihen und Fourierintegrale" Dokl. Akad. Nauk SSSR , 102 (1955) pp. 1073–1076 |
| [a5] | E.M. Stein, "Harmonic analysis" , Princeton Univ. Press (1993) |
| [a6] | S. Thangavelu, "Lectures on Hermite and Laguerre expansions" , Princeton Univ. Press (1993) |
| [a7] | C. Sogge, "On the convergence of Riesz means on compact manifolds" Ann. of Math. , 126 (1987) pp. 439–447 |
Bochner-Riesz means. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bochner-Riesz_means&oldid=16536