Bernstein method

method of auxiliary functions

A method which is employed in the theory of linear and non-linear partial differential equations. Bernstein's method consists in introducing certain new (auxiliary) functions, which depend on the solution being sought, and which make it possible to establish a priori estimates of the maximum modulus of the derivatives of this solution of the required order.

A simple example of the application of Bernstein's method is the a priori estimate of the modulus of the derivatives of the solution of the Dirichlet problem for the non-linear (quasi-linear) elliptic equation

(*)

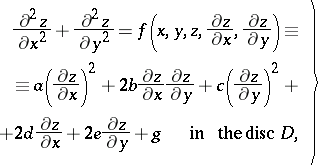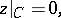where 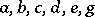are smooth functions of 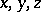; 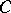is the circle, the boundary of the disc 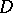with radius 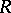(the assumption to the effect that 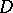is a disc and 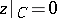is immaterial, since the general case of an arbitrary-connected domain and inhomogeneous boundary condition is readily reduced to the case under consideration by a change of the function and a conformal transformation of the domain).

If 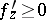, then the estimated maximum modulus

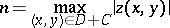of the solution of problem (*) is immediately obtained from the maximum principle.

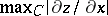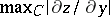In order to prove that a regular solution of problem (*) exists it is sufficient to have a priori estimates of the maximum modulus of the derivatives of the solution up to the third order (cf. Continuation method (to a parametrized family)). To estimate and , it is sufficient to estimate 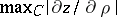(since 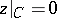), where 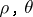are polar coordinates in the disc 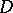. Now introduce a new (auxiliary) function , given by the formula

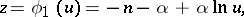where 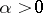will be selected later. The function 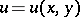varies from to 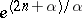in the same direction as 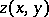(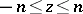). Since

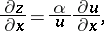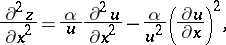and similar results for derivatives with respect to , it follows that satisfies the equation

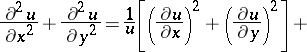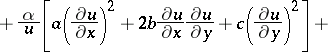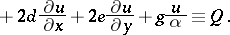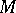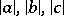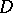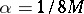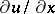Let be the upper bound of in , and let . If and 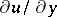are considered as current coordinates in the plane, and 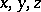as parameters, the equation 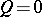is the equation of an ellipse, since the determinant 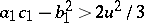, where

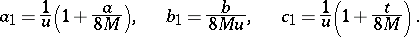Thus, for any 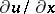and 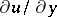, 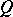will not be smaller than a certain negative number 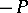, 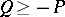(the number 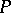is readily obtained in explicit form). If one introduces the function 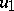given by the formula

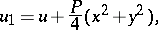one obtains

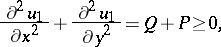and 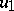attains its maximum on the boundary 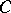of the domain 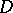and, since 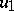is constant on 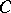, one has

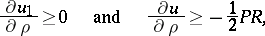where 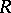is the radius of the circle 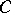. Hence it is possible to find a negative lower bound for :

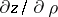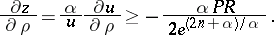If the same reasoning is applied to a second auxiliary function

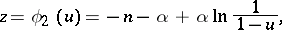one obtains an estimate from above

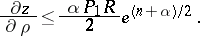Thus, 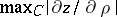is estimated, which means that 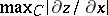and 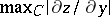are estimated as well. The estimate of the maximum modulus of the first derivatives inside the domain 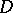is performed in a similar manner: introduce an auxiliary function given by the formula

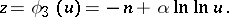The function varies in the same direction as , from to 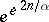. In view of (*), on may write the following expression for

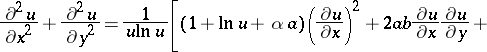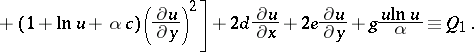Considerations similar to those given above show that if the function

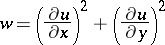attains a maximum in the domain 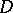, this maximum does not exceed some number, the value of which depends solely on and 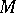. This yields the required estimates of 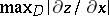and .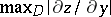

Bernstein's method may also be used to estimate, in a similar manner, the maximum modulus in the domain 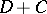of all highest derivatives of the solution (the only other operation which is required is the differentiation of the initial equation).

The method was first utilized by S.N. Bernstein [e theory of functions','../c/c025430.htm','Continuation method (to a parametrized family)','../c/c025520.htm','Euler–Lagrange equation','../e/e036510.htm','Fourier series','../f/f041090.htm','Functions of a real variable, theory of','../f/f042130.htm','Hilbert problems','../h/h120080.htm','Jackson inequality','../j/j054000.htm','Laplace theorem','../l/l057530.htm','Lebesgue constants','../l/l057800.htm','Limit theorems','../l/l058920.htm','Linear elliptic partial differential equation and system','../l/l059180.htm','Lyapunov theorem','../l/l061200.htm','Mathematical statistics','../m/m062710.htm','Minimal surface','../m/m063920.htm','Markov–Bernstein-type inequalities','../m/m110060.htm','Ornstein–Uhlenbeck process','../o/o070240.htm','Orthogonal polynomials','../o/o070340.htm','Plateau problem, multi-dimensional','../p/p072850.htm','Quasi-analytic class','../q/q076370.htm')" style="background-color:yellow;">S.N. Bernshtein] . The method was subsequently extended and was systematically utilized in the study of various problems for elliptic and parabolic differential operators [3], [4], [5].

References

[1a]	S.N. [S.N. Bernshtein] Bernstein, "Sur la généralisation du problème de Dirichlet (première partie)" Math. Ann. , 62 (1906) pp. 253–271
[1b]	S.N. [S.N. Bernshtein] Bernstein, "Sur la généralisation du problème de Dirichlet (deuxième partie)" Math. Ann. , 69 (1910) pp. 82–136
[2]	S.N. Bernshtein, , Collected works , 3 , Moscow (1960)
[3]	O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian)
[4]	A.V. Pogorelov, "Die Verbiegung konvexer Flächen" , Akademie Verlag (1957) (Translated from Russian)
[5]	O.A. Oleinik, S.N. Kruzhkov, "Quasi-linear parabolic equations of second order in several independent variables" Russian Math. Surveys , 16 : 2 (1961) pp. 105–146 Uspekhi Mat. Nauk , 16 : 5 (1961) pp. 115–155