The sequence of rational numbers 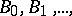 discovered by Jacob Bernoulli [1] in connection with the calculation of the sum of equal powers of natural numbers:
discovered by Jacob Bernoulli [1] in connection with the calculation of the sum of equal powers of natural numbers:
The values of the first Bernoulli numbers are:
All odd-indexed Bernoulli numbers except for 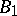 are zero, and the signs of
are zero, and the signs of 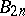 alternate. Bernoulli numbers are the values of the Bernoulli polynomials at
alternate. Bernoulli numbers are the values of the Bernoulli polynomials at 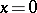 :
:  ; they also often serve as the coefficients of the expansions of certain elementary functions into power series. Thus, for example,
; they also often serve as the coefficients of the expansions of certain elementary functions into power series. Thus, for example,
(the so-called generating function of the Bernoulli numbers);
L. Euler in 1740 pointed out the connection between Bernoulli numbers and the values of the Riemann zeta-function 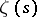 for even
for even 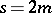 :
:
Bernoulli numbers are used to express many improper integrals, such as
Certain relationships involving Bernoulli numbers are:
(the recurrence formula);
The estimates:
hold. Extensive tables of Bernoulli numbers are available; for instance, [2] contains accurate values of 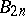 for
for 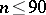 and approximate values for
and approximate values for 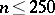 .
.
Bernoulli numbers have found many applications in mathematical analysis, number theory and approximate calculations.
References
| [1] | J. Bernoulli, "Ars conjectandi" , Werke , 3 , Birkhäuser (1975) pp. 107–286 (Original: Basle, 1713) |
| [2] | H.T. Davis, "Tables of the higher mathematical functions" , 2 , Bloomington (1935) |
| [3] | L. Saalschuetz, "Vorlesungen über die Bernoullischen Zahlen" , Berlin (1893) |
| [4] | I.I. Chistyakov, "Bernoulli numbers" , Moscow (1895) (In Russian) |
| [5] | N. Nielsen, "Traité élémentaire de nombres de Bernoulli" , Paris (1923) |
| [6] | V.A. Kudryavtsev, "Summation of powers of natural numbers and Bernoulli numbers" , Moscow-Leningrad (1936) (In Russian) |
| [7] | N.E. Nörlund, "Volesungen über Differenzenrechnung" , Springer (1924) |
| [8] | A.O. [A.O. Gel'fond] Gelfond, "Differenzenrechnung" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
| [9] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
Bernoulli numbers play an important role in the theory of cyclotomic fields and Fermat's last theorem, see [a1], pp. 40-41, and [a2]. E.g., if 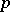 is an odd prime number that does not divide the numerators of
is an odd prime number that does not divide the numerators of  , then
, then 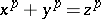 has no solutions in
has no solutions in 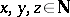 . (See also Cyclotomic field; Fermat great theorem.)
. (See also Cyclotomic field; Fermat great theorem.)
References
| [a1] | S. Lang, "Cyclotomic fields" , Springer (1978) |
| [a2] | P. Ribenboim, "Thirteen lectures on Fermat's last theorem" , Springer (1979) |
How to Cite This Entry:
Bernoulli numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_numbers&oldid=15872
This article was adapted from an original article by Yu.N. Subbotin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article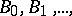 discovered by Jacob Bernoulli [1] in connection with the calculation of the sum of equal powers of natural numbers:
discovered by Jacob Bernoulli [1] in connection with the calculation of the sum of equal powers of natural numbers:
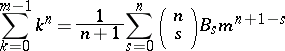


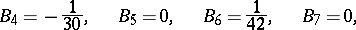

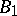 are zero, and the signs of
are zero, and the signs of 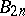 alternate. Bernoulli numbers are the values of the Bernoulli polynomials at
alternate. Bernoulli numbers are the values of the Bernoulli polynomials at 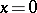 :
:  ; they also often serve as the coefficients of the expansions of certain elementary functions into power series. Thus, for example,
; they also often serve as the coefficients of the expansions of certain elementary functions into power series. Thus, for example,
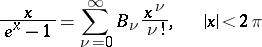
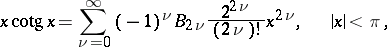
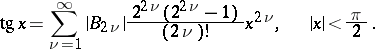
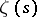 for even
for even 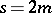 :
:
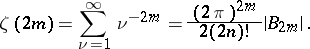
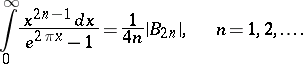
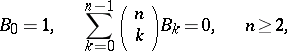
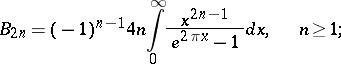
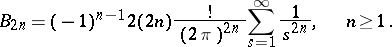
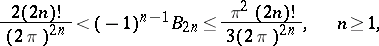
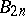 for
for 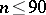 and approximate values for
and approximate values for 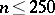 .
.
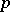 is an odd prime number that does not divide the numerators of
is an odd prime number that does not divide the numerators of  , then
, then 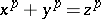 has no solutions in
has no solutions in 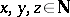 . (See also Cyclotomic field; Fermat great theorem.)
. (See also Cyclotomic field; Fermat great theorem.)