Banach-Mazur game
A game that appeared in the famous Scottish Book [a11], [a6], where its initial version was formulated as Problem 43 by the Polish mathematician S. Mazur: Given the space of real numbers 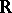 and a non-empty subset
and a non-empty subset 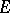 of it, two players
of it, two players 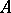 and
and 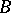 play a game in the following way:
play a game in the following way: 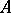 starts by choosing a non-empty interval
starts by choosing a non-empty interval 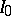 of
of 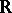 and then
and then  responds by choosing a non-empty subinterval
responds by choosing a non-empty subinterval 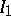 of
of 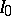 . Then player
. Then player 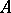 in turn selects a non-empty interval
in turn selects a non-empty interval 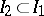 and
and 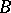 continues by taking a non-empty subinterval
continues by taking a non-empty subinterval 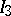 of
of  . This procedure is iterated infinitely many times. The resulting infinite sequence of nested intervals
. This procedure is iterated infinitely many times. The resulting infinite sequence of nested intervals 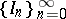 is called a play. By definition, the player
is called a play. By definition, the player 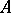 wins this play if the intersection
wins this play if the intersection 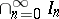 has a common point with
has a common point with 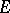 . Otherwise
. Otherwise 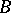 wins. Mazur had observed two facts:
wins. Mazur had observed two facts:
a) if the complement of 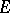 in some interval of
in some interval of 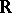 is of the first Baire category in this interval (equivalently, if
is of the first Baire category in this interval (equivalently, if 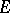 is residual in some interval of
is residual in some interval of 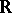 , cf. also Category of a set; Baire classes), then player
, cf. also Category of a set; Baire classes), then player 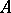 has a winning strategy (see below for the definition); and
has a winning strategy (see below for the definition); and
b) if 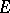 itself is of the first Baire category in
itself is of the first Baire category in 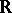 , then
, then 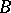 has a winning strategy. The question originally posed by Mazur in Problem 43 of the Scottish Book (with as prize a bottle of wine!) was whether the inverse implications in the above two assertions hold. On August 4, 1935, S. Banach wrote in the same book that "Mazur's conjecture is true" . The proof of this statement of Banach however has never been published. The game subsequently became known as the Banach–Mazur game.
has a winning strategy. The question originally posed by Mazur in Problem 43 of the Scottish Book (with as prize a bottle of wine!) was whether the inverse implications in the above two assertions hold. On August 4, 1935, S. Banach wrote in the same book that "Mazur's conjecture is true" . The proof of this statement of Banach however has never been published. The game subsequently became known as the Banach–Mazur game.
More than 20 years later, in 1957, J. Oxtoby [a8] published a proof for the validity of Mazur's conjecture. Oxtoby considered a much more general setting. The game was played in a general topological space 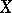 with
with  and the two players
and the two players 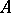 and
and 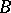 were choosing alternatively sets
were choosing alternatively sets 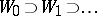 from an a priori prescribed family of sets
from an a priori prescribed family of sets 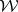 which has the property that every element of
which has the property that every element of 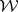 contains a non-empty open subset of
contains a non-empty open subset of 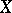 and every non-empty open subset of
and every non-empty open subset of 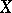 contains an element of
contains an element of  . As above,
. As above, 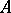 wins if
wins if 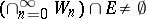 , otherwise
, otherwise 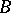 wins. Oxtoby's theorem says that
wins. Oxtoby's theorem says that 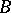 has a winning strategy if and only if
has a winning strategy if and only if 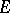 is of the first Baire category in
is of the first Baire category in 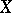 ; also, if
; also, if 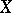 is a complete metric space, then
is a complete metric space, then 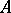 has a winning strategy exactly when
has a winning strategy exactly when 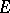 is residual in some non-empty open subset of
is residual in some non-empty open subset of 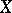 .
.
Later, the game was subjected to different generalizations and modifications.
Generalizations.
Only the most popular modification of this game will be considered. It has turned out to be useful not only in set-theoretic topology, but also in the geometry of Banach spaces, non-linear analysis, number theory, descriptive set theory, well-posedness in optimization, etc. This modification is the following: Given a topological space 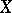 , two players (usually called
, two players (usually called 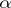 and
and 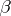 ) alternatively choose non-empty open sets
) alternatively choose non-empty open sets 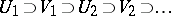 (in this sequence the
(in this sequence the  are the choices of
are the choices of 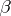 and the
and the 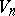 are the choices of
are the choices of 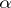 ; thus, it is player
; thus, it is player 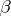 who starts this game). Player
who starts this game). Player 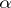 wins the play
wins the play 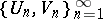 if
if 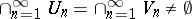 , otherwise
, otherwise 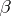 wins. To be completely consistent with the general scheme described above, one may think that
wins. To be completely consistent with the general scheme described above, one may think that 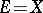 and
and  starts by always choosing the whole space
starts by always choosing the whole space 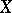 . This game is often denoted by
. This game is often denoted by 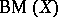 .
.
A strategy  for the player
for the player 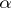 is a mapping which assigns to every finite sequence
is a mapping which assigns to every finite sequence 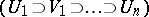 of legal moves in
of legal moves in  a non-empty open subset
a non-empty open subset 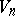 of
of 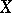 included in the last move of
included in the last move of  (i.e.
(i.e. 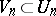 ). A stationary strategy (called also a tactics) for
). A stationary strategy (called also a tactics) for 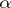 is a strategy for this player which depends only on the last move of the opponent. A winning strategy (a stationary winning strategy)
is a strategy for this player which depends only on the last move of the opponent. A winning strategy (a stationary winning strategy)  for
for 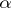 is a strategy such that
is a strategy such that 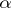 wins every play in which his/her moves are obtained by
wins every play in which his/her moves are obtained by  . Similarly one defines the (winning) strategies for
. Similarly one defines the (winning) strategies for 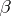 .
.
A topological space 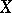 is called weakly
is called weakly  -favourable if
-favourable if 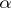 has a winning strategy in
has a winning strategy in 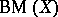 , while it is termed
, while it is termed 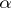 -favourable if there is a stationary winning strategy for
-favourable if there is a stationary winning strategy for 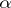 in
in 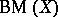 . It can be derived from the work of Oxtoby [a8] (see also [a4], [a7] and [a9]) that the space
. It can be derived from the work of Oxtoby [a8] (see also [a4], [a7] and [a9]) that the space 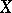 is a Baire space exactly when player
is a Baire space exactly when player 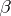 does not have a winning strategy in
does not have a winning strategy in 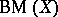 . Hence, every weakly
. Hence, every weakly 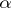 -favourable space is a Baire space. In the class of metric spaces
-favourable space is a Baire space. In the class of metric spaces 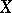 , a metric space is weakly
, a metric space is weakly 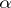 -favourable if and only if it contains a dense and completely metrizable subspace. One can use these two results to see that the Banach–Mazur game is "not determined" . I.e. it could happen for some space
-favourable if and only if it contains a dense and completely metrizable subspace. One can use these two results to see that the Banach–Mazur game is "not determined" . I.e. it could happen for some space 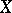 that neither
that neither 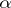 nor
nor 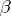 has a winning strategy. For instance, the Bernstein set
has a winning strategy. For instance, the Bernstein set 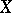 in the real line (cf. also Non-measurable set) is a Baire space which does not contain a dense completely metrizable subspace (consequently
in the real line (cf. also Non-measurable set) is a Baire space which does not contain a dense completely metrizable subspace (consequently 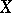 does not admit a winning strategy for either
does not admit a winning strategy for either 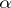 or
or 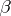 ).
).
The above characterization of weak 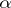 -favourability for metric spaces has been extended for some non-metrizable spaces in [a10].
-favourability for metric spaces has been extended for some non-metrizable spaces in [a10].
A characterization of 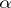 -favourability of a given completely-regular space
-favourability of a given completely-regular space 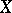 can be obtained by means of the space
can be obtained by means of the space 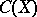 of all continuous and bounded real-valued functions on
of all continuous and bounded real-valued functions on 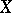 equipped with the usual sup-norm
equipped with the usual sup-norm 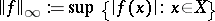 . The following statement holds [a5]: The space
. The following statement holds [a5]: The space 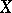 is weakly
is weakly 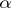 -favourable if and only if the set
-favourable if and only if the set
 |
is residual in 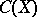 . In other words,
. In other words, 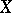 is weakly
is weakly 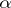 -favourable if and only if almost-all (from the Baire category point of view) of the functions in
-favourable if and only if almost-all (from the Baire category point of view) of the functions in 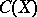 attain their maximum in
attain their maximum in 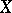 . The rich interplay between
. The rich interplay between 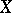 ,
, 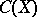 and
and 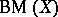 is excellently presented in [a3].
is excellently presented in [a3].
The class of 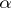 -favourable spaces (spaces which admit
-favourable spaces (spaces which admit 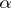 -winning tactics) is strictly narrower than the class of weakly
-winning tactics) is strictly narrower than the class of weakly 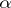 -favourable spaces. G. Debs [a2] has exhibited a completely-regular topological space
-favourable spaces. G. Debs [a2] has exhibited a completely-regular topological space 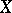 which admits a winning strategy for
which admits a winning strategy for  in
in 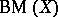 , but does not admit any
, but does not admit any 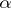 -winning tactics in
-winning tactics in 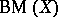 . Under the name "espaces tamisables" , the
. Under the name "espaces tamisables" , the 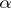 -favourable spaces were introduced and studied also by G. Choquet [a1].
-favourable spaces were introduced and studied also by G. Choquet [a1].
[a10] is an excellent survey paper about topological games (including 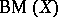 ).
).
References
| [a1] | G. Choquet, "Une classe régulières d'espaces de Baire" C.R. Acad. Sci. Paris Sér. I , 246 (1958) pp. 218–220 |
| [a2] | G. Debs, "Strategies gagnantes dans certain jeux topologique" Fundam. Math. , 126 (1985) pp. 93–105 |
| [a3] | G. Debs, J. Saint-Raymond, "Topological games and optimization problems" Mathematika , 41 (1994) pp. 117–132 |
| [a4] | M.R. Krom, "Infinite games and special Baire space extensions" Pacific J. Math. , 55 : 2 (1974) pp. 483–487 |
| [a5] | P.S. Kenderov, J.P. Revalski, "The Banach–Mazur game and generic existence of solutions to optimization problems" Proc. Amer. Math. Soc. , 118 (1993) pp. 911–917 |
| [a6] | "The Scottish Book: Mathematics from the Scottish Café" R.D. Mauldin (ed.) , Birkhäuser (1981) |
| [a7] | R.A. McCoy, "A Baire space extension" Proc. Amer. Math. Soc. , 33 (1972) pp. 199–202 |
| [a8] | J. Oxtoby, "The Banach–Mazur game and the Banach category theorem" , Contributions to the Theory of Games III , Ann. of Math. Stud. , 39 , Princeton Univ. Press (1957) pp. 159–163 |
| [a9] | J. Saint-Raymond, "Jeux topologiques et espaces de Namioka" Proc. Amer. Math. Soc. , 87 (1983) pp. 499–504 |
| [a10] | R. Telgárski, "Topological games: On the fifth anniversary of the Banach–Mazur game" Rocky Mount. J. Math. , 17 (1987) pp. 227–276 |
| [a11] | S.M. Ulam, "The Scottish Book" , A LASL monograph , Los Alamos Sci. Lab. (1977) (Edition: Second) |
Banach-Mazur game. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach-Mazur_game&oldid=15639