Balanced set
From Encyclopedia of Mathematics
A set 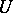 in a real or complex vector space
in a real or complex vector space 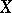 such that
such that 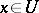 and
and 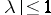 imply
imply 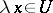 . An example of a balanced set is given by the unit ball in a normed vector space and, generally, by a neighbourhood
. An example of a balanced set is given by the unit ball in a normed vector space and, generally, by a neighbourhood 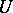 of zero in a base of neighbourhoods of zero in a topological vector space. These neighbourhoods of zero are moreover absorbing, i.e. such that for any
of zero in a base of neighbourhoods of zero in a topological vector space. These neighbourhoods of zero are moreover absorbing, i.e. such that for any 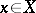 there exists an
there exists an 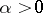 such that
such that 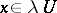 for
for 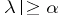 . If
. If 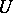 is a convex, absorbing and balanced set, then the functional
is a convex, absorbing and balanced set, then the functional 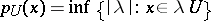 is a semi-norm, i.e. it has the properties
is a semi-norm, i.e. it has the properties
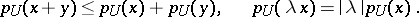 |
A balanced set is also called centred.
References
| [1] | L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1982) (Translated from Russian) |
Comments
The functional 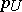 mentioned above is also called the Minkowski functional of the convex, absorbing and balanced set
mentioned above is also called the Minkowski functional of the convex, absorbing and balanced set 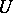 .
.
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 |
How to Cite This Entry:
Balanced set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Balanced_set&oldid=18616
Balanced set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Balanced_set&oldid=18616
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article