Arrangement of hyperplanes
Let  be an
be an  -dimensional affine space over the field
-dimensional affine space over the field  . An arrangement of hyperplanes,
. An arrangement of hyperplanes,  , is a finite collection of codimension-one affine subspaces in
, is a finite collection of codimension-one affine subspaces in  , [a5].
, [a5].
Examples of arrangements of hyperplanes.
1) A subset of the coordinate hyperplanes is called a Boolean arrangement.
2) An arrangement is in general position if at each point it is locally Boolean.
3) The braid arrangement consists of the hyperplanes  . It is the set of reflecting hyperplanes of the symmetric group on
. It is the set of reflecting hyperplanes of the symmetric group on  letters.
letters.
4) The reflecting hyperplanes of a finite reflection group.
Combinatorics.
An edge  of
of  is a non-empty intersection of elements of
is a non-empty intersection of elements of 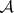 . Let
. Let  be the set of edges partially ordered by reverse inclusion. Then
be the set of edges partially ordered by reverse inclusion. Then  is a geometric semi-lattice with minimal element
is a geometric semi-lattice with minimal element  , rank given by codimension, and maximal elements of the same rank,
, rank given by codimension, and maximal elements of the same rank,  . The Möbius function on
. The Möbius function on 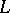 is defined by
is defined by  and, for
and, for 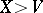 ,
,
 |
The characteristic polynomial of 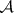 is
is  . Let
. Let  . For a generic arrangement of
. For a generic arrangement of  hyperplanes,
hyperplanes,
 |
For the braid arrangement,
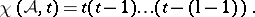 |
Similar factorizations hold for all reflection arrangements involving the (co)exponents of the reflection group. Given a 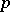 -tuple of hyperplanes,
-tuple of hyperplanes, 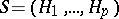 , let
, let 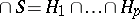 ; note that
; note that 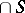 may be empty. One says that
may be empty. One says that 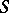 is dependent if
is dependent if 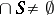 and
and 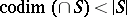 . Let
. Let 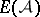 be the exterior algebra on symbols
be the exterior algebra on symbols 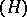 for
for 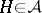 , where the product is juxtaposition. Define
, where the product is juxtaposition. Define 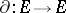 by
by 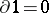 ,
, 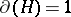 and, for
and, for 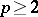 ,
,
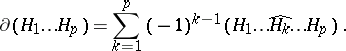 |
Let  be the ideal of
be the ideal of 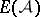 generated by
generated by  . The Orlik–Solomon algebra of
. The Orlik–Solomon algebra of  is
is 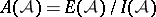 . For connections with matroid theory, see [a3].
. For connections with matroid theory, see [a3].
Divisor.
The divisor of 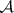 is the union of the hyperplanes, denoted by
is the union of the hyperplanes, denoted by  . If
. If 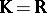 or
or  , then
, then 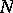 has the homotopy type of a wedge of
has the homotopy type of a wedge of 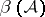 spheres of dimension
spheres of dimension 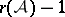 , [a4]. The singularities of
, [a4]. The singularities of  are not isolated. The divisor of a general-position arrangement has normal crossings, but this is not true for arbitrary
are not isolated. The divisor of a general-position arrangement has normal crossings, but this is not true for arbitrary 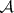 . Blowing-up
. Blowing-up 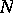 along all edges where it is not locally a product of arrangements yields a normal crossing divisor. See also Divisor.
along all edges where it is not locally a product of arrangements yields a normal crossing divisor. See also Divisor.
Complement.
The complement of 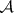 is
is 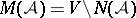 .
.
1) If  , then
, then  is a finite set of cardinality
is a finite set of cardinality 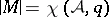 .
.
2) If  , then
, then 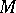 is a disjoint union of open convex sets (chambers) of cardinality
is a disjoint union of open convex sets (chambers) of cardinality  . If
. If 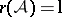 ,
, 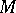 contains
contains  chambers with compact closure, [a7].
chambers with compact closure, [a7].
3) If 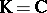 , then
, then 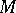 is an open complex (Stein) manifold of the homotopy type of a finite CW-complex (cf. also Stein manifold). Its cohomology is torsion-free and its Poincaré polynomial (cf. Künneth formula) is
is an open complex (Stein) manifold of the homotopy type of a finite CW-complex (cf. also Stein manifold). Its cohomology is torsion-free and its Poincaré polynomial (cf. Künneth formula) is 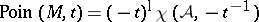 . The product structure is determined by the isomorphism of graded algebras
. The product structure is determined by the isomorphism of graded algebras  . The fundamental group of
. The fundamental group of  has an effective presentation, but the higher homotopy groups of
has an effective presentation, but the higher homotopy groups of 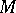 are not known in general.
are not known in general.
The complement of a Boolean arrangement is a complex torus. In a general-position arrangement of 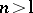 hyperplanes,
hyperplanes, 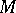 has non-trivial higher homotopy groups. For the braid arrangement,
has non-trivial higher homotopy groups. For the braid arrangement, 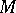 is called the pure braid space and its higher homotopy groups are trivial. The symmetric group acts freely on
is called the pure braid space and its higher homotopy groups are trivial. The symmetric group acts freely on  with as orbit space the braid space whose fundamental group is the braid group. The quotient of the divisor by the symmetric group is called the discriminant, which has connections with singularity theory.
with as orbit space the braid space whose fundamental group is the braid group. The quotient of the divisor by the symmetric group is called the discriminant, which has connections with singularity theory.
Ball quotients.
Examples of algebraic surfaces whose universal cover is the complex ball were constructed as "Kummer" covers of the projective plane branched along certain arrangements of projective lines, [a2].
Logarithmic forms.
For 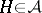 , choose a linear polynomial
, choose a linear polynomial 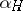 with
with  and let
and let  . Let
. Let 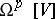 denote all global regular (i.e., polynomial)
denote all global regular (i.e., polynomial) 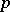 -forms on
-forms on  . Let
. Let 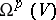 denote the space of all global rational
denote the space of all global rational 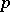 -forms on
-forms on 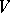 . The space
. The space  of logarithmic
of logarithmic  -forms with poles along
-forms with poles along 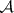 is
is
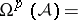 |
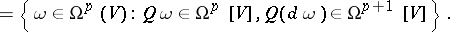 |
The arrangement is free if 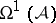 is a free module over the polynomial ring. A free arrangement
is a free module over the polynomial ring. A free arrangement  has integer exponents
has integer exponents 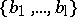 , so that
, so that  . Reflection arrangements are free. This explains the factorization of their characteristic polynomials.
. Reflection arrangements are free. This explains the factorization of their characteristic polynomials.
Hypergeometric integrals.
Certain rank-one local system cohomology groups of 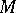 may be identified with spaces of hypergeometric integrals, [a1]. If the local system is suitably generic, these cohomology groups may be computed using the algebra
may be identified with spaces of hypergeometric integrals, [a1]. If the local system is suitably generic, these cohomology groups may be computed using the algebra  . Only the top cohomology group is non-zero, and it has dimension
. Only the top cohomology group is non-zero, and it has dimension 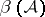 . See [a6] for connections with the representation theory of Lie algebras and quantum groups, and with the Knizhnik–Zamolodchikov differential equations of physics.
. See [a6] for connections with the representation theory of Lie algebras and quantum groups, and with the Knizhnik–Zamolodchikov differential equations of physics.
References
| [a1] | K. Aomoto, M. Kita, "Hypergeometric functions" , Springer (1994) (Translated from Japanese) MR2799182 MR2482635 MR1866164 MR1805969 MR1792063 MR1768923 MR1803881 MR1749398 MR1614401 MR1401610 MR1256465 MR0988314 Zbl 1229.33001 Zbl 1169.33307 Zbl 1174.33301 Zbl 1189.33028 Zbl 0972.33009 Zbl 0927.33014 Zbl 0943.32010 Zbl 0787.33001 Zbl 0859.33001 |
| [a2] | G. Barthel, F. Hirzebruch, T. Höfer, "Geradenkonfigurationen und Algebraische Flächen" , Vieweg (1987) MR0912097 Zbl 0645.14016 |
| [a3] | A. Björner, M. Las Vergnas, B. Sturmfels, N. White, G.M. Ziegler, "Oriented matroids" , Cambridge Univ. Press (1993) MR1226888 Zbl 0773.52001 |
| [a4] | M. Goresky, R. MacPherson, "Stratified Morse theory" , Springer (1988) MR0932724 Zbl 0639.14012 |
| [a5] | P. Orlik, H. Terao, "Arrangements of hyperplanes" , Springer (1992) MR1217488 Zbl 0757.55001 |
| [a6] | A. Varchenko, "Multidimensional hypergeometric functions and representation theory of Lie algebras and quantum groups" , World Sci. (1995) MR1384760 Zbl 0951.33001 |
| [a7] | T. Zaslavsky, "Facing up to arrangements: face-count formulas for partitions of space by hyperplanes" , Memoirs , 154 , Amer. Math. Soc. (1975) MR0357135 Zbl 0296.50010 |
Arrangement of hyperplanes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arrangement_of_hyperplanes&oldid=24369