Approximation solvability
A-solvability
Let 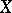 and
and 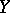 be Banach spaces (cf. also Banach space), let
be Banach spaces (cf. also Banach space), let 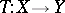 be a, possibly non-linear, mapping (cf. also Non-linear operator) and let
be a, possibly non-linear, mapping (cf. also Non-linear operator) and let 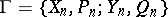 be an admissible scheme for
be an admissible scheme for 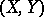 , which, for simplicity, is assumed to be a complete projection scheme, i.e.
, which, for simplicity, is assumed to be a complete projection scheme, i.e. 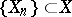 and
and 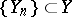 are finite-dimensional subspaces with
are finite-dimensional subspaces with 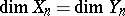 for each
for each  and
and 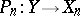 and
and 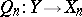 are linear projections such that
are linear projections such that 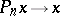 and
and 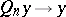 for
for 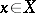 and
and 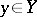 . Clearly, such schemes exist if both
. Clearly, such schemes exist if both 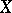 and
and 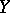 have a Schauder basis (cf. also Basis; Biorthogonal system). Consider the equation
have a Schauder basis (cf. also Basis; Biorthogonal system). Consider the equation
 | (a1) |
One of the basic problems in functional analysis is to "solve" (a1). Here, "solvability" of (a1) can be understood in (at least) two manners:
A) solvability in which a solution 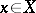 of (a1) is somehow established; or
of (a1) is somehow established; or
B) approximation solvability of (a1) (with respect to 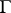 ), in which a solution
), in which a solution 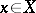 of (a1) is obtained as the limit (or at least, a limit point) of solutions
of (a1) is obtained as the limit (or at least, a limit point) of solutions 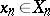 of finite-dimensional approximate equations:
of finite-dimensional approximate equations:
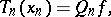 | (a2) |
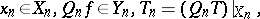 |
with 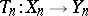 continuous for each
continuous for each  . If
. If 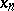 and
and  are unique, then (a1) is said to be uniquely A-solvable.
are unique, then (a1) is said to be uniquely A-solvable.
Although the concepts A) and B) are distinct in their purpose, they are not independent. In fact, sometimes knowledge of A) is essential for B) to take place.
If 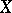 and
and  are Hilbert spaces (cf. Hilbert space), the projections
are Hilbert spaces (cf. Hilbert space), the projections 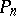 and
and 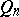 are assumed to be orthogonal (cf. Orthogonal projector). If, for example,
are assumed to be orthogonal (cf. Orthogonal projector). If, for example, 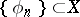 and
and 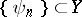 are orthogonal bases, then
are orthogonal bases, then 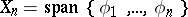 and
and  , and
, and 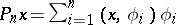 and
and 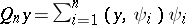 for
for 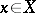 ,
, 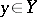 . In this case, setting
. In this case, setting 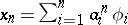 , the coefficients
, the coefficients 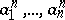 are determined by (a2), which reduces to the system
are determined by (a2), which reduces to the system
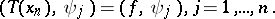 |
A-proper.
In studying the A-solvability of (a1) one may ask: For what type of linear or non-linear mapping 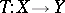 is it possible to show that (a1) is uniquely A-solvable? It turns out that the notion of an A-proper mapping is essential in answering this question.
is it possible to show that (a1) is uniquely A-solvable? It turns out that the notion of an A-proper mapping is essential in answering this question.
A mapping 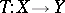 is called A-proper if and only if
is called A-proper if and only if 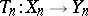 is continuous for each
is continuous for each  and such that if
and such that if 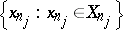 is any bounded sequence satisfying
is any bounded sequence satisfying  for some
for some 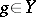 , then there exist a subsequence
, then there exist a subsequence 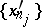 and an
and an 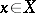 such that
such that 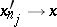 as
as 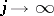 and
and 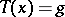 , as was first shown in [a2].
, as was first shown in [a2].
It was found (see [a1]) that there are intimate relationships between (unique) A-solvability and A-properness of 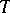 , shown by the following results:
, shown by the following results:
R1) If 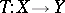 is a continuous linear mapping, then (a1) is uniquely A-solvable if and only if
is a continuous linear mapping, then (a1) is uniquely A-solvable if and only if  is A-proper and one-to-one. This is the best possible result, which includes as a special case all earlier results for the Galerkin or Petrov–Galerkin method (cf. also Galerkin method).
is A-proper and one-to-one. This is the best possible result, which includes as a special case all earlier results for the Galerkin or Petrov–Galerkin method (cf. also Galerkin method).
R2) If 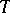 is non-linear and
is non-linear and
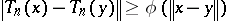 | (a3) |
for all 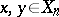 ,
, 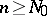 , where
, where 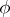 is a continuous function on
is a continuous function on 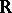 with
with 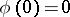 ,
, 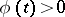 for
for 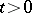 and
and  as
as 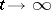 , then (a1) is uniquely A-solvable for each
, then (a1) is uniquely A-solvable for each 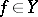 if and only if
if and only if 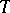 is A-proper and one-to-one. If
is A-proper and one-to-one. If 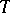 is continuous, then R2) holds without the condition that
is continuous, then R2) holds without the condition that 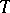 be one-to-one. The result R2) includes various results for strongly monotone or strongly accretive mappings (cf. also Accretive mapping). If
be one-to-one. The result R2) includes various results for strongly monotone or strongly accretive mappings (cf. also Accretive mapping). If 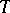 is a continuous linear mapping, then (a3) reduces to
is a continuous linear mapping, then (a3) reduces to
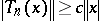 | (a4) |
for all 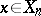 ,
, 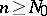 , and some
, and some 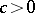 . If, in addition, the scheme
. If, in addition, the scheme 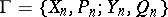 is nested, i.e.
is nested, i.e. 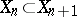 and
and 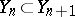 for all
for all  , and
, and 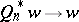 in
in 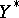 for each
for each 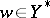 , then
, then 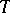 is A-proper and one-to-one if and only if (a4) holds. In particular, by R1), equation (a1) is uniquely A-solvable for each
is A-proper and one-to-one if and only if (a4) holds. In particular, by R1), equation (a1) is uniquely A-solvable for each 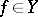 . Without this extra condition on
. Without this extra condition on 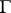 , equation (a1) is uniquely A-solvable if (a1) is solvable for each
, equation (a1) is uniquely A-solvable if (a1) is solvable for each 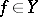 , or if either
, or if either 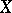 or
or 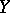 is reflexive (cf. also Reflexive space).
is reflexive (cf. also Reflexive space).
References
| [a1] | W.V. Petryshyn, "Approximation-solvability of nonlinear functional and differential equations" , Monographs , 171 , M. Dekker (1993) |
| [a2] | W.V. Petryshyn, "On projectional-solvability and Fredholm alternative for equations involving linear A-proper operators" Arch. Rat. Anal. , 30 (1968) pp. 270–284 |
Approximation solvability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximation_solvability&oldid=15238