Anisotropic group
over a field 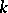
A linear algebraic group 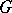 defined over
defined over 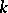 and of
and of 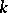 -rank zero, i.e. not containing non-trivial
-rank zero, i.e. not containing non-trivial 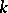 -split tori (cf. Splittable group). Classical examples of anisotropic groups include the orthogonal groups of quadratic forms that do not vanish over
-split tori (cf. Splittable group). Classical examples of anisotropic groups include the orthogonal groups of quadratic forms that do not vanish over 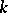 ; and algebraic groups of elements of reduced norm one in division algebras over
; and algebraic groups of elements of reduced norm one in division algebras over 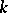 . If
. If 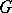 is semi-simple, and if the characteristic of
is semi-simple, and if the characteristic of 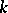 is zero, then
is zero, then 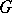 is anisotropic over
is anisotropic over 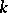 if and only if
if and only if 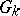 contains non-trivial unipotent elements. (For the field of real numbers or the field of
contains non-trivial unipotent elements. (For the field of real numbers or the field of 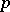 -adic numbers this is equivalent to saying that
-adic numbers this is equivalent to saying that 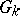 is compact.) The classification of arbitrary semi-simple groups over the field
is compact.) The classification of arbitrary semi-simple groups over the field 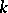 reduces essentially to the classification of anisotropic groups.
reduces essentially to the classification of anisotropic groups.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | J. Tits, "Classification of algebraic simple groups" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 33–62 |
Anisotropic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anisotropic_group&oldid=14493