Analytic geometry
A branch of geometry. The fundamental concepts of analytic geometry are the simplest geometric elements (points, straight lines, planes, second-order curves and surfaces). The principal means of study in analytic geometry are the method of coordinates and the methods of elementary algebra. The genesis of the method of coordinates is closely linked with the intense development of astronomy, mechanics and technology in the 17th century. In his Géometrie, R. Descartes (1637) gave a clear and exhaustive account of this method and of the foundations of analytic geometry. P. Fermat, a contemporary of Descartes, was also familiar with the principles of this method. Subsequent development of analytic geometry is due to the studies of G. Leibniz, I. Newton and, particularly, L. Euler. The tools of analytic geometry were utilized by J.L. Lagrange in his construction of analytic mechanics and by G. Monge in differential geometry. In our own days, analytic geometry has no significance as an independent branch of science, but its methods are extensively employed in various fields of mathematics, mechanics, physics and other sciences.
The principle of the method of coordinates is as follows. Consider, for example, two mutually-perpendicular straight lines 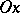 and
and 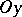 in a plane
in a plane 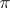 . These lines, including their direction, the coordinate origin
. These lines, including their direction, the coordinate origin 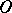 and the selected scale unit
and the selected scale unit  , form a so-called Cartesian orthogonal system
, form a so-called Cartesian orthogonal system 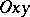 of coordinates on the plane. The straight lines
of coordinates on the plane. The straight lines 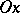 and
and 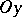 are called the abscissa (axis) and the ordinate (axis) respectively. The location of any point
are called the abscissa (axis) and the ordinate (axis) respectively. The location of any point 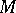 in the plane relative to this system
in the plane relative to this system 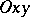 can be determined as follows. Let
can be determined as follows. Let 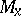 and
and 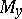 be the projections of
be the projections of 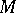 onto
onto 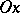 and
and 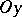 , and let the numbers
, and let the numbers  and
and 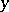 be the magnitudes of the segments
be the magnitudes of the segments 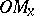 and
and 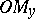 (the magnitude
(the magnitude  of the segment
of the segment 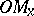 , for example, is equal to the length of this segment, taken with the plus sign if the direction from
, for example, is equal to the length of this segment, taken with the plus sign if the direction from 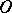 to
to 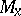 is the same as the direction of the straight line
is the same as the direction of the straight line 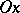 , and taken with the minus sign in the opposite case). The numbers
, and taken with the minus sign in the opposite case). The numbers  (the abscissa) and
(the abscissa) and 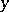 (the ordinate) are said to be the Cartesian orthogonal coordinates of the point
(the ordinate) are said to be the Cartesian orthogonal coordinates of the point 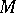 in the system
in the system 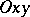 . A point
. A point 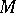 with abscissa
with abscissa  and ordinate
and ordinate 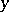 is denoted by the symbol
is denoted by the symbol 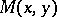 . The coordinates of a point
. The coordinates of a point 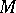 clearly determine its location with respect to the system
clearly determine its location with respect to the system 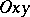 .
.
Let a line 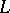 be given on a plane
be given on a plane 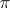 with a given Cartesian orthogonal coordinate system
with a given Cartesian orthogonal coordinate system 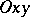 . Using the concept of coordinates of a point it is possible to introduce the concept of the equation of the line
. Using the concept of coordinates of a point it is possible to introduce the concept of the equation of the line 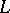 with respect to system
with respect to system 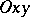 as an equation of the type
as an equation of the type 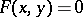 , which will be satisfied by the coordinates
, which will be satisfied by the coordinates  and
and  of any point
of any point 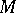 on
on 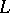 , but not by those of any point which does not lie on
, but not by those of any point which does not lie on 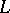 .
.
The basic idea of the method of coordinates on a plane is that the geometric properties of the line 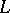 can be clarified by studying its equation
can be clarified by studying its equation 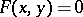 by analytic and algebraic tools. Thus, for instance, the problem of the number of intersection points between a straight line and a circle is reduced to the analytic problem of the number of solutions of the set of equations of the line and of the circle.
by analytic and algebraic tools. Thus, for instance, the problem of the number of intersection points between a straight line and a circle is reduced to the analytic problem of the number of solutions of the set of equations of the line and of the circle.
This was in fact the method of study of the properties of an ellipse, a hyperbola and a parabola, which are the lines of intersection between a circular cone and planes which do not pass through its vertex (cf. Conic sections).
The so-called algebraic curves of the first and second orders are a subject of systematic study in plane analytic geometry; in Cartesian orthogonal coordinates these are described by algebraic equations of the first and second degree, respectively. The curves of the first order are rectilinear and, conversely, any straight line is described by an algebraic equation 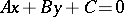 of the first degree. The curves of the second order are described by equations of the form
of the first degree. The curves of the second order are described by equations of the form 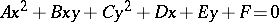 . The principal technique in the study and classification of such curves is to select a Cartesian orthogonal coordinate system in which the equation assumes its simplest form, after which the simple equation is studied. Cf. Second-order curve.
. The principal technique in the study and classification of such curves is to select a Cartesian orthogonal coordinate system in which the equation assumes its simplest form, after which the simple equation is studied. Cf. Second-order curve.
In the analytic geometry of space, the Cartesian orthogonal coordinates are 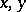 and
and  (the abscissa, the ordinate and the applicate), and points
(the abscissa, the ordinate and the applicate), and points  are described exactly as in plane analytic geometry. Any given surface
are described exactly as in plane analytic geometry. Any given surface 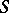 in space has its own equation
in space has its own equation  in the coordinate system
in the coordinate system 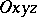 , and its geometric properties are studied by studying its equation by analytic and algebraic means. A curve
, and its geometric properties are studied by studying its equation by analytic and algebraic means. A curve 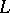 in space is given as the intersection of two surfaces
in space is given as the intersection of two surfaces 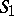 and
and 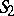 . If the respective equations of
. If the respective equations of 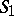 and
and 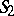 are
are 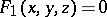 and
and 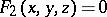 , these equations, considered together, are the equation of the curve
, these equations, considered together, are the equation of the curve 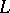 . Thus, a straight line
. Thus, a straight line 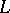 in space may be considered as the intersection of two planes. In analytic geometry of space a systematic study is made of the so-called algebraic surfaces of the first and second orders. It was found that only planes are algebraic surfaces of the first order. Surfaces of the second order have equations of the type
in space may be considered as the intersection of two planes. In analytic geometry of space a systematic study is made of the so-called algebraic surfaces of the first and second orders. It was found that only planes are algebraic surfaces of the first order. Surfaces of the second order have equations of the type
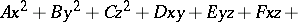 |
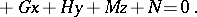 |
The principal method of study and classification of such surfaces is to select a Cartesian coordinate system in which the equation of the surface assumes its simplest form, the latter being then studied. Cf. Surface of the second order.
References
| [1] | R. Descartes, "La géometrie" , Leiden (1637) |
| [2] | H. Wieleitner, "Die Geschichte der Mathematik von Descartes bis zum Hälfte des 19. Jahrhunderts" , de Gruyter (1923) |
| [3] | N.V. Efimov, "A short course of analytical geometry" , Moscow (1967) (In Russian) |
| [4] | V.A. Il'in, E.G. Poznyak, "Analytical geometry" , MIR (1984) (Translated from Russian) |
| [5] | P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian) |
| [6] | M.M. Postnikov, "Analytic geometry" , Moscow (1973) (In Russian) |
| [7] | S.V. Bakhvalov, P.S. Modenov, A.S. Parkhomenko, "Collection of problems on analytic geometry" , Moscow (1964) (In Russian) |
Comments
References
| [a1] | G. Bol, "Elemente der analytischen Geometrie" , Vandenhoeck & Ruprecht (1948) |
| [a2] | K. Borsuk, "Analytic geometry" , PWN (1969) |
| [a3] | D.J. Struik, "Lectures on analytic and projective geometry" , Addison-Wesley (1953) pp. 157–160 |
| [a4] | J.A. Todd, "Projective and analytical geometry" , Pitman (1947) pp. Chapt. VI |
Analytic geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_geometry&oldid=15081