Almost-split sequence
Auslander–Reiten sequence
Roughly speaking, almost-split sequences are minimal non-split short exact sequences. They were introduced by M. Auslander and I. Reiten in 1974–1975 and have become a central tool in the theory of representations of finite-dimensional algebras (cf. also Representation of an associative algebra).
Let 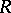 be an Artin algebra, i.e.
be an Artin algebra, i.e. 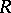 is an associative ring with unity that is finitely generated as a module over its centre
is an associative ring with unity that is finitely generated as a module over its centre 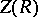 , which is a commutative Artinian ring.
, which is a commutative Artinian ring.
Let 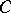 be an indecomposable non-projective finitely-generated left
be an indecomposable non-projective finitely-generated left 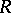 -module. Then there exists a short exact sequence
-module. Then there exists a short exact sequence
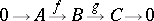 | (a1) |
in 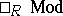 , the category of finitely-generated left
, the category of finitely-generated left  -modules, with the following properties:
-modules, with the following properties:
i) 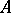 and
and 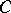 are indecomposable;
are indecomposable;
ii) the sequence does not split, i.e. there is no section 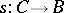 of
of 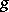 (a homomorphism such that
(a homomorphism such that 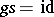 ), or, equivalently, there is no retraction of
), or, equivalently, there is no retraction of 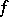 (a homomorphism
(a homomorphism 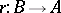 such that
such that 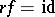 );
);
iii) given any 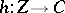 with
with 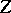 indecomposable and
indecomposable and 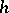 not an isomorphism, there is a lift of
not an isomorphism, there is a lift of 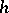 to
to 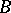 (i.e. a homomorphism
(i.e. a homomorphism 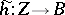 in
in 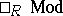 such that
such that 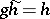 );
);
iv) given any 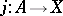 with
with 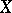 indecomposable and
indecomposable and 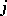 not an isomorphism, there is a homomorphism
not an isomorphism, there is a homomorphism 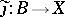 such that
such that 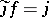 .
.
Note that if iii) (or, equivalently, iv)) were to hold for all 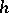 , not just those
, not just those 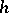 that are not isomorphisms, the sequence (a1) would be split, whence "almost split" . Moreover, a sequence (a1) with these properties is uniquely determined (up to isomorphism) by
that are not isomorphisms, the sequence (a1) would be split, whence "almost split" . Moreover, a sequence (a1) with these properties is uniquely determined (up to isomorphism) by 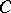 , and also by
, and also by 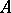 . This is the basic Auslander–Reiten theorem on almost-split sequences, [a1], [a8], [a9], [a10], [a11].
. This is the basic Auslander–Reiten theorem on almost-split sequences, [a1], [a8], [a9], [a10], [a11].
For convenience (things also work more generally), let now  be a finite-dimensional algebra over an algebraically closed field
be a finite-dimensional algebra over an algebraically closed field 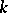 . The category
. The category  is a Krull–Schmidt category (Krull–Remak–Schmidt category), i.e. a
is a Krull–Schmidt category (Krull–Remak–Schmidt category), i.e. a 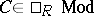 is indecomposable if and only if
is indecomposable if and only if 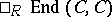 , the endomorphism ring of
, the endomorphism ring of 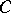 , is a local ring and (hence) the decomposition of a module in
, is a local ring and (hence) the decomposition of a module in 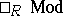 into indecomposables is unique up to isomorphism.
into indecomposables is unique up to isomorphism.
Let 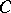 be an indecomposable and consider the contravariant functor
be an indecomposable and consider the contravariant functor 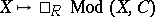 . The morphisms
. The morphisms 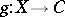 that do not admit a section (i.e. an
that do not admit a section (i.e. an 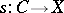 such that
such that 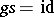 ) form a vector subspace
) form a vector subspace 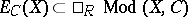 . Let
. Let 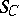 be the quotient functor
be the quotient functor 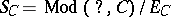 . Then, for an indecomposable
. Then, for an indecomposable 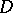 ,
, 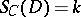 if
if 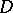 is isomorphic to
is isomorphic to 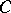 and zero otherwise. So
and zero otherwise. So 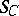 is a simple functor. (All functors
is a simple functor. (All functors 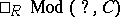 ,
, 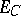 ,
, 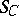 are viewed as
are viewed as  -functors, i.e. functors that take their values in the category of vector
-functors, i.e. functors that take their values in the category of vector 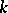 -spaces.) If
-spaces.) If 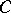 is indecomposable, then (the Auslander–Reiten theorem, [a4], p.4) the simple functor
is indecomposable, then (the Auslander–Reiten theorem, [a4], p.4) the simple functor 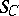 admits a minimal projective resolution of the form
admits a minimal projective resolution of the form
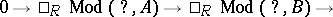 |
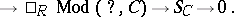 |
If 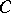 is projective,
is projective, 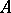 is zero, otherwise
is zero, otherwise 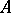 is indecomposable.
is indecomposable.
If 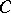 is not projective, the sequence
is not projective, the sequence 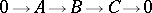 is exact and is the almost-split sequence determined by
is exact and is the almost-split sequence determined by  .
.
This functorial definition is used in [a5] in the somewhat more general setting of exact categories.
For a good introduction to the use of almost-split sequences, see [a6]; see also [a3], [a5] for comprehensive treatments. See also Riedtmann classification for the use of almost-split sequences and the Auslander–Reiten quiver in the classification of self-injective algebras.
The Bautista–Brunner theorem says that if 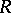 is of finite representation type and
is of finite representation type and 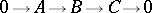 is an almost-split sequence, then
is an almost-split sequence, then 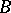 has at most
has at most 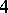 terms in its decomposition into indecomposables; also, if there are indeed
terms in its decomposition into indecomposables; also, if there are indeed 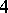 , then one of these is projective-injective. This can be generalized, [a7].
, then one of these is projective-injective. This can be generalized, [a7].
References
| [a1] | M. Auslander, I. Reiten, "Stable equivalence of dualizing  -varieties I" Adv. Math. , 12 (1974) pp. 306–366 -varieties I" Adv. Math. , 12 (1974) pp. 306–366 |
| [a2] | M. Auslander, "The what, where, and why of almost split sequences" , Proc. ICM 1986, Berkeley , I , Amer. Math. Soc. (1987) pp. 338–345 |
| [a3] | M. Auslander, I. Reiten, S.O. Smalø, "Representation theory of Artin algebras" , Cambridge Univ. Press (1995) |
| [a4] | P. Gabriel, "Auslander–Reiten sequences and representation-finite algebras" V. Dlab (ed.) P. Gabriel (ed.) , Representation Theory I. Proc. Ottawa 1979 Conf. , Springer (1980) pp. 1–71 |
| [a5] | P. Gabriel, A.V. Roiter, "Representations of finite-dimensional algebras" , Springer (1997) pp. Sect. 9.3 |
| [a6] | I. Reiten, "The use of almost split sequences in the representation theory of Artin algebras" M. Auslander (ed.) E. Lluis (ed.) , Representation of Algebras. Proc. Puebla 1978 Workshop , Springer (1982) pp. 29–104 |
| [a7] | Shiping Liu, "Almost split sequenes for non-regular modules" Fundam. Math. , 143 (1993) pp. 183–190 |
| [a8] | M. Auslander, I. Reiten, "Representation theory of Artin algebras III" Commun. Algebra , 3 (1975) pp. 239–294 |
| [a9] | M. Auslander, I. Reiten, "Representation theory of Artin algebras IV" Commun. Algebra , 5 (1977) pp. 443–518 |
| [a10] | M. Auslander, I. Reiten, "Representation theory of Artin algebras V" Commun. Algebra , 5 (1977) pp. 519–554 |
| [a11] | M. Auslander, I. Reiten, "Representation theory of Artin algebras VI" Commun. Algebra , 6 (1978) pp. 257–300 |
Almost-split sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Almost-split_sequence&oldid=12003