Algebraic algebra
An algebra 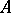 with associative powers (in particular, an associative algebra) over a field
with associative powers (in particular, an associative algebra) over a field 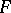 all elements of which are algebraic (an element
all elements of which are algebraic (an element  is called algebraic if the subalgebra
is called algebraic if the subalgebra 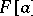 generated by it is finite-dimensional or, equivalently, if the element
generated by it is finite-dimensional or, equivalently, if the element  has an annihilating polynomial with coefficients from the ground field
has an annihilating polynomial with coefficients from the ground field 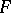 ). An algebra
). An algebra 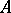 is called an algebraic algebra of bounded degree if it is algebraic and if the set of degrees of the minimal annihilating polynomials of its elements is bounded. Subalgebras and homomorphic images of an algebraic algebra (of bounded degree) are algebraic algebras (of bounded degree).
is called an algebraic algebra of bounded degree if it is algebraic and if the set of degrees of the minimal annihilating polynomials of its elements is bounded. Subalgebras and homomorphic images of an algebraic algebra (of bounded degree) are algebraic algebras (of bounded degree).
Examples: locally finite algebras (in particular, finite-dimensional ones), nil-algebras and associative skew-fields with a countable set of generators over an uncountable field.
The algebras considered below are associative. The Jacobson radical of an algebraic algebra is a nil-ideal. A primitive algebraic algebra 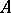 is isomorphic to a dense algebra of linear transformations of a vector space over a skew-field; if, in addition,
is isomorphic to a dense algebra of linear transformations of a vector space over a skew-field; if, in addition, 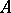 is of bounded degree, then
is of bounded degree, then 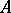 is isomorphic to a ring of matrices over a skew-field. An algebraic algebra without non-zero nilpotent elements (in particular, a skew-field) over a finite field is commutative. It follows that finite skew-fields are commutative. An algebraic algebra of bounded degree satisfies a polynomial identity (cf. PI-algebra). An algebraic PI-algebra is locally finite. If the ground field is uncountable, then the algebras obtained from an algebraic algebra by extension of the ground field, and the tensor product of algebraic algebras, are algebraic algebras.
is isomorphic to a ring of matrices over a skew-field. An algebraic algebra without non-zero nilpotent elements (in particular, a skew-field) over a finite field is commutative. It follows that finite skew-fields are commutative. An algebraic algebra of bounded degree satisfies a polynomial identity (cf. PI-algebra). An algebraic PI-algebra is locally finite. If the ground field is uncountable, then the algebras obtained from an algebraic algebra by extension of the ground field, and the tensor product of algebraic algebras, are algebraic algebras.
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [2] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) |
Algebraic algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_algebra&oldid=15135